1660 캡틴 이다솜 (백준, python3)

 

시간 제한	메모리 제한
2초	128MB

문제

캡틴 이다솜은 자신의 해적선에 적을 공격하기 위한 대포알을 많이 보관해 놓는다. 다솜이는 미적감각이 뛰어나기 때문에, 대포알은 반드시 사면체 모양으로 쌓아놓아야 한다고 생각한다. 사면체를 만드는 방법은 길이가 N인 정삼각형 모양을 만든다. 그 위에 길이가 N-1인 정삼각형 모양을 얹고 그위에 계속 해서 얹어서 1크기의 정삼각형 모양을 얹으면 된다.

예를 들어, 사이즈가 3크기의 한 더미 모양은 다음과 같다.

    X

    X
  X  X

    X
  X  X
X  X  X

각각의 삼각형은 1, 3, 6, 10 ,..... 와 같이 대포알을 가지고 있다. 따라서 완벽하게 쌓았을 때, 한 사면체에는 1, 4, 10, 20 ,.... 개를 가지고 있을 것이다.

현재 다솜이의 해적선에 대포알이 N개가 있다. 다솜이는 영식이를 시켜서 사면체를 만들게 하고 싶다. 영식이는 물론 하기 싫지만 어쩔수 없이 다솜이가 시키는대로 사면체를 가능한 최소 개수 만큼 만들려고 한다. N개의 대포알로 만들 수 있는 사면체의 최소 개수를 출력하는 프로그램을 작성하시오.

 

입력

첫째 줄에 입력 N이 들어온다. N은 300,000보다 작거나 같은 자연수이다.

 

출력

첫째 줄에 영식이가 만들 수 있는 사면체 개수의 최솟값을 출력한다.

 

---

풀이

최대 300,000개의 대포알로 만들 수 있는 가장 큰 하나의 사면체 사이즈부터 구해보자. 사면체에 필요한 대포알의 수는 이렇다.

사이즈	식	대포알 수
1	1	1
2	1+(1+2)	4
3	1+(1+2)+(1+2+3)	10
4	1+(1+2)+(1+2+3)+(1+2+3+4)	20
...	...	...
n	?	?

각 사이즈에 필요한 대포알의 수는 대충 아래와 같이 표현할 수 있다.

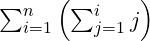
식을 풀어서 정리해보면 다음과 같다.

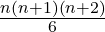
n이 얼마이면 30만을 넘는가? 121이다. 계산해보니 121 사이즈는 302,621개의 대포알을 필요로 한다. 따라서 이 문제에서는 120 사이즈 까지만 구해보면 모든 해를 다 얻을 수 있다.

 

처음에는 30만까지의 모든 경우를 사이즈 1의 사면체 만으로 구성해본다. dp[i] = i일 것이다. 그 다음으로는 사이즈 2의 사면체로 값을 줄여준다. dp[4]는 사이즈 1의 사면체로는 4개의 사면체가 필요하지만 사이즈 2의 사면체를 사용하면 1개로 줄일 수 있다. dp[5]도 원래 5개지만 사이즈 1과 사이즈 2를 각각 1개씩 사용해 2개의 사면체로 줄여줄 수 있다. 이렇게 사이즈 i인 사면체의 대포알 수를 t라고 했을 때, t부터 30만까지의 경우 dp[j]는 dp[j - t] + 1로 바꿔줄 수도 있다. 항상 바꿔주는 것이 정답은 아니므로 각각의 시행마다 비교해서 값을 정해준다. 점화식을 아래와 같이 정리할 수 있다.

# 사이즈 i의 사면체에 필요한 대포알의 수 t에 대하여
# j를 t부터 30만까지 1씩 증가시키며 다음 식을 실행한다.
dp[j] = min(dp[j], dp[j - t] + 1)

어딘가 최적화가 가능할 것 같지만 꾸역꾸역 2304ms로 통과가 됐다. 파이썬으로 188ms 컷 낸 사람이 있긴 하던데 급수의 급수를 쳐다보고 있으니 머리 아파서 그냥 넘어가기로...

 

정답 코드

import sys
input = sys.stdin.readline
def solution():
    N = int(input())
    dp = [300000] * 300001
    dp[0] = 0
    k = 1
    t = k
    for i in range(2, 122):
        k += i
        for j in range(t, 300001):
            if dp[j] > dp[j - t] + 1:
                dp[j] = dp[j - t] + 1
        t += k
    print(dp[N])
solution()