1. 정점이 용량을 갖는 유량 그래프
최대유량 문제에서는 간선으로 용량 정보가 주어진다. 근데 만약 정점에 용량이 있다면? 음의 유량 처리 과정에 문제가 생긴다.
포드 풀커슨의 방법에서 가장 핵심적인 아이디어는 음의 유량을 만들어 기존 유량을 우회시키는 테크닉이다.
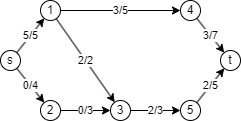
정점 중심으로 생각해보면 정점 3은 나가는 방향의 간선 용량의 총합인 3의 용량을 갖는다고 할 수 있다. 1→3의 유량 2를 우회시키면 s-2-3-5-t에 2의 유량을 흘려보낼 수 있다. 여기서 유량 우회가 가능한 이유는 유량을 간선 정보로 관리하고 있기 때문이다. u-v 간선 용량을 capa[u][v], u-v 간선의 현재 유량을 flow[u][v] 라고 표현하면 그래프 자체에서 u와 v의 순서로 간선의 방향 정보를 모두 관리하고 있는 셈이다.
그런데 정점에 용량을 정해둔다면 유량도 역시 정점에서 관리해야 한다. 문제는 어떤 간선을 타고 온 유량인지 알 수 없다는 것이다. 정점 내에서 유량 정보를 배열로 관리한다고 하면 간선 정보를 저장할 공간이 2배가 된다는 공간 복잡도 상의 문제가 생길 수 있다.(정점, 간선 수가 적으면 가능한 방법인 것 같긴 하다.)
2. 정점 분할
그럼 이제 유량 그래프에서 간선에는 용량을 설정할 수 있지만 정점에는 용량을 설정할 수 없다는 특징이 나타난다. 이걸 이용하면 정점에 용량을 설정할 수 있는데 바로 정점을 간선으로 만들어버리는 것이다. 하나의 정점을 둘로 나누어버리고 그 사이를 간선으로 연결하면 그 간선에 용량을 설정할 수 있다. 이러면 하나의 정점은 입구와 출구가 생기는 셈이다. 입구로 탐색이 들어온다 해도 정점 내부 간선의 용량이 이미 가득 찼다면 출구로 나갈 수 없는 식이다.

이렇게 되면 in, out 으로 분리된 정점 내에 간선이 생성되었고 용량은 1이다. 이 정점을 지나는 유량이 1 생성되면 이 간선이 가득차게 되고 이 정점을 통과할 수 없다. 당연히 음의 유량도 정상적으로 생성되고 유량 우회도 가능하다.
이제 해야 할 일은 2배로 늘어난 정점 정보를 관리하는 것이다. 만약 정점 번호가 1부터 N까지 였다면, 2N개의 정점이 필요하게 된다. i번 정점을 i와 N+i로 나누든, i*2-1과 i*2로 나누든 분할된 정점 내부의 간선을 연결해주고 한 정점은 다른 정점에서 들어오는 방향, 다른 정점은 나가는 방향으로 잘 연결해주면 된다.
3. 관련 문제
1, 2번을 제외한 도시는 1번만 방문해야 한다. 도시마다 용량이 1로 제한되어야 하는 것이기 때문에 모든 도시를 정점 분할해, 용량이 1인 간선을 끼워 넣어주면 된다.
시간의 흐름이 있다. 유량마다 시간 정보를 따로 관리하기에는 너무 복잡하기 때문에 모든 도시를 시간으로 정점 분할 해버린다. 예를 들어 5번 도시에서 6번 도시로 넘어갈 때 시간이 3 소요된다고 해보자. 5번 도시에 4의 시간에 도착한 유량이 있을 때, 이 유량이 6번 도시로 넘어가면 6번 도시의 7의 시간에 도착하는 것이다. 그리고 각 도시에서 시간을 보내는 것이 가능하기 때문에 분할된 도시들은 시간 순으로 무한한 용량을 갖는 간선으로 모두 연결되어야 한다.
