| 시간 제한 | 메모리 제한 |
| 1초 | 1024MB |
문제
고려대학교는 특이하게 매일 첫 번째 수업을 시작할 때부터 마지막 수업이 끝날 때까지 비가 온다고 한다. 비 맞는 것을 싫어하는 근호는 학교 건물을 연결하는 길목들에 거대한 파라솔을 설치하여 비를 피하려고 한다.
고려대학교는 아래와 같이 N개의 건물이 일렬로 배치된 형태이다. 왼쪽에 있는 건물부터 순서대로 1번 건물, 2번 건물, ···, N번 건물이고, 인접한 건물 사이에는 두 건물을 직접 연결하는 길목이 있다. 파라솔은 각 길목당 하나씩 설치할 수 있으며, 파라솔이 설치된 길목은 지나갈 때 비를 맞지 않는다.

근호는 한 학기 동안 고려대학교에서 수업을 들을 것이다. 한 학기는 M일이고, i(1 ≤ i ≤ M)번째 날에는 Ai번 건물부터 Bi번 건물 사이에 있는 건물들에서 수업을 듣는다. 근호가 i번째 날에 비를 맞지 않으려면 i번째 날 수업을 듣기 전에 Ai번 건물과 Bi번 건물 사이에 있는 모든 길목에 파라솔이 설치되어 있어야 한다.
그래서 근호는 학기 중 매일 아침, 등교해서 수업을 듣기 전에 원하는 길목에 파라솔을 설치하기로 했다. 파라솔을 설치하는 데는 시간이 걸리기 때문에, 매일 아침에 설치할 수 있는 파라솔의 개수는 최대 1개이다.
하지만 근호는 매일 아침에 파라솔을 설치하는 것만으로는 수업 시간표에 맞춰 파라솔을 모두 설치할 수 없을 것임을 깨닫고, 학기가 시작되기 전에 미리 파라솔을 몇 개 설치하려고 한다.
근호가 한 학기 동안 비를 한 번도 맞지 않으려면 학기가 시작되기 전에 최소 몇 개의 길목에 파라솔을 미리 설치해야 하는가? 처음에는 모든 길목에 파라솔이 설치되어 있지 않고, 한 번 설치한 파라솔은 학기가 끝날 때까지 설치된 상태를 유지한다.
입력
첫 번째 줄에 고려대학교의 건물 개수 N과 한 학기의 일 수 M이 공백으로 구분되어 정수로 주어진다. (1 ≤ N ≤ 500,000; 1 ≤ M ≤ 1,000,000)
이후 M개의 줄에 걸쳐 근호의 수업 시간표가 주어진다. i+1번째 줄에는 정수 Ai, Bi가 주어진다. (1 ≤ Ai ≤ Bi ≤ N)
입력되는 데이터의 양이 많음에 유의하자.
출력
첫 번째 줄에 근호가 개강 전에 파라솔을 설치해야 하는 길목의 최소 개수를 출력한다.
풀이
가장 나이브한 풀이를 생각해보자. 최대 499,999개의 위치에 대해 최대 1,000,000번의 선형탐색을 실시해 파라솔이 비어있는 자리가 몇 개인지 알 수 있다. 일단 여기서 연산 횟수가 약 5000억 번으로 가볍게 시간초과가 되겠다. 일단 선형 탐색은 아닌 셈이다. A와 B 구간 사이에 파라솔이 비어있는 자리를 빠르게 찾아낼 수 있다면 좋을텐데...
파라솔로 연결된 건물들을 하나의 덩어리로 보고 그 모든 건물들의 오른쪽 끝 건물의 번호를 대표로 지정해주면 어떨까? 그러면 어떤 구간 A~B가 주어졌을 때, A의 대표 건물이 B보다 작은지 아닌지 알아보는 것으로 파라솔의 필요 여부를 알 수 있다.
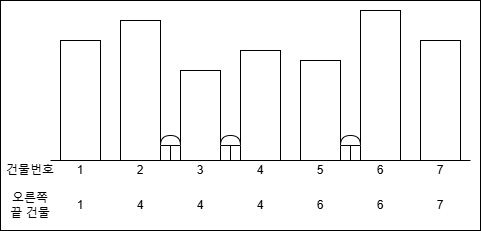
이런 상태의 건물이 있다고 해보자. 오른쪽 끝 건물의 번호까지 지정되어있다. 만약 여기서 2~5구간을 확인한다면 2번 건물의 대표 건물인 4번으로 보고, 4번이 5번과 연결되지 않았으므로 1개의 파라솔이 필요하다는 것을 알 수 있다. 4번 건물의 다음 번호는 5번이고 대표 건물이 6번이다. 원하는 구간을 넘어갔으니 여기서는 파라솔이 더 필요하지 않다. 각 건물들이 누구와 연결되어있는지 기록하는 분리집합이 만들어지는 셈이다. Union find의 시간복잡도는 평균 O(logN)이므로, 최악의 경우 O(Q * logN), 20,000,000번 정도의 연산이면 문제 해결이 가능하다.
그런데 하루에 1개의 파라솔을 설치할 수 있다고 했다. 만약 어떤 날에 주어진 구간에서 파라솔이 설치될 필요가 없다면, 설치 가능한 파라솔 1개를 킵할 수 있다. 다음 날엔 두 개 설치가 가능한 셈이다. 이런 식으로 날마다 설치 가능한 파라솔의 수를 1씩 증가시키고, 필요한 파라솔의 수를 킵해둔 파라솔의 수에서 감산하되 필요한 파라솔의 양이 더 많다면 방학에 미리 설치해야 할 파라솔의 수를 부족한 만큼 증가시키면 된다.
정답 코드
import sys
input = sys.stdin.readline
def solution():
N, M = map(int, input().split())
linked = [i for i in range(N + 1)]
parasol = 0
day = 0
for _ in range(M):
day += 1
need = 0
a, b = map(int, input().split())
while a < b:
while linked[a] > a:
k = linked[a]
linked[a] = max(linked[a], b)
a = k
if a < b:
need += 1
linked[a] = b
a += 1
if need <= day:
day -= need
else:
parasol += need - day
day = 0
print(parasol)
solution()
