1655번: 가운데를 말해요
첫째 줄에는 백준이가 외치는 정수의 개수 N이 주어진다. N은 1보다 크거나 같고, 100,000보다 작거나 같은 자연수이다. 그 다음 N줄에 걸쳐서 백준이가 외치는 정수가 차례대로 주어진다. 정수는 -1
www.acmicpc.net
IDEA
자료를 입력 받음과 동시에 정렬을 해내야하는 문제다. 중앙값을 입력과 동시에 최신화 해주어야하기 때문에 자료는 항상 중앙값에 한해 정렬된 상태를 유지한다. "어떤 자료 구조를 사용하고 어떻게 입력을 받아 정렬 상태를 유지해낼 것이냐"가 이 문제의 빡센 0.1초의 시간 제한을 뚫을 수 있냐 없냐를 결정하는 문제다.
먼저 일반적인 배열을 떠올렸다. 가장 작은 값이 맨 앞으로 오는 오름차순 정렬을 유지한다. 매 N번째 입력마다 Binary Search로 O(log N)에 삽입할 위치를 찾고 O(N)에 정렬을 끝낼 수 있다. 그럼 이 방법을 이용한다면 O(N2 + log N!)에 결과를 얻을 수 있다.(맞나? 맞을 거다. 아마도.) 구현은 쉽겠지만 0.1초 안에는 절대 결과를 얻을 수 없을 것 같다. 이렇게 자료의 위치를 뒤로 쭉쭉 밀어줘야하는 문제 때문에 Queue, Stack 역시 후보에서 배제됐다.
두 번째로 생각한 방법은 Linked List였다. 대충 듣기만 했던 자료구조라 이걸 이용하면 최소한 새 자료를 삽입하고 그 뒤의 값들을 하나씩 밀어낼 때 걸릴 시간은 절약할 수 있다. 하지만 역시 O(N + log N!)은 0.1초와 거리가 멀다.
세 번째로 찾은 방법은 최소, 최대 힙이었다. 힙 자료구조는 트리의 형태를 가지며 입력과 동시에 정렬이 끝난다. 정렬은 이진탐색의 원리가 적용되기 때문에 탐색과 동시에 자료의 정렬이 끝나는 식이다. 힙의 모든 자료는 두 개의 하위 노드를 가지며 최소 힙은 최상위에 있는 자료가 가장 작은 값을 갖는다. 최대 힙은 반대다. 최대 힙에 새 자료가 들어간다면 힙의 마지막 값 다음 위치에 새 값이 저장된다. 그리고 새로 저장된 값은 상위 노드와 값을 비교해 더 큰 값이 위로 가도록 위치를 바꾼다. 바꿀 필요가 없다면 정렬이 끝난 상태다.

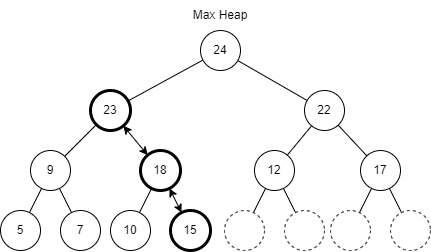
최대 힙에서 어떤 값이 빠진다면 그 위치에 힙의 마지막 값을 가져온다. 그리고 이번에는 반대로 2개의 하위 노드와 비교해 그중 가장 큰 값이 상위 노드로 오도록 위치를 바꾼다. 바꿀 필요가 없다면 정렬이 끝난 상태다.

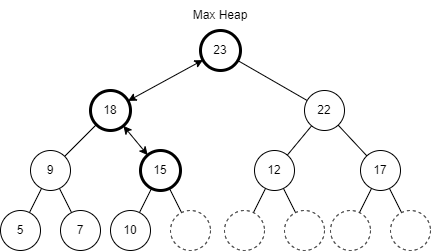
만약 어떤 자료를 하나의 힙에 저장한다면 최대 힙의 경우 항상 가장 큰 값을 알 수 있고, 최소 힙의 경우 항상 가장 작은 값을 알 수 있다. 그런데 이 문제에서 필요한 값은 중앙값이다. 여기서 군대에서 탄약고 근무 서다 사수가 나에게 냈던 퀴즈가 생각났다.
"파란색 조끼를 입은 사람 5명과 빨간색 조끼를 입은 사람 5명이 있다. 이 사람들이 무작위로 튀어나가 열을 이루는데 딱 하나의 조건만 알려주고 색깔이 섞이지 않게 줄세우려고 한다. 어떤 조건을 말해줘야 할까?"
한 5분 정도 고민하다가 답이 생각났었다.
"이미 서있는 줄에 빨강과 파랑의 경계가 있다면 그 경계 사이에 끼어서고 없으면 아무데나 서라."
사실 최소, 최대 힙을 이용한 중앙값을 찾는 것과는 거리가 좀 있는데 그냥 이 답을 떠올렸을 때 머릿 속에 상상했던 이미지가 뭔가 이 문제에 맞물리면서 최소 힙과 최대 힙을 동시에 사용하는 장면이 생각났다. 모든 자료들을 중앙값을 기준으로 그보다 큰 값은 최소 힙으로, 그보다 작은 값은 최대 힙으로 정렬해주면 문제가 원하는 답은 항상 최대 힙의 최상위 값이 된다. 이 방법이라면 O(log N!)안에 결과를 얻을 수 있다.

힙은 모든 자료가 1개의 부모 노드와 2개의 자식 노드를 갖기 때문에 차례로 번호를 붙여주면 하위 노드의 번호는 부모 노드의 번호가 i 일 때 각각 i * 2, i * 2 + 1 이라는 특징을 갖는다. 힙의 길이만 따로 관리해준다면 배열로 간단히 구현할 수 있다. 알고리즘은 다음과 같이 정리할 수 있다.
1. i 번째 값을 입력 받는다.
2. i % 2 == 0 이라면 3으로, 1이라면 4로 이동한다.
3. 만약 입력 받은 값이 최소 힙의 최상위 값보다 크다면 최소 힙의 최상위 값을 최대 힙에 새로 삽입하고 입력받은 값은 최소 힙의 최상위에 저장해 자식노드와 비교해 위치를 바꾸어 내려가며 정렬하고 5로 이동한다.
4. 만약 입력 받은 값이 최대 힙의 최상위 값보다 작다면 최대 힙의 최상위 값을 최소 힙에 새로 삽입하고 입력받은 값은 최대 힙의 최상위에 저장해 자식노드와 비교해 위치를 바꾸어 내려가며 정렬하고 5로 이동한다.
5. 최대 힙의 최상위 값을 출력한다.
6. i가 N 보다 작으면 1로 돌아가고 N이라면 프로그램을 종료한다.
CODE
using System;
using System.IO;
using System.Linq;
class Program
{
static int N, index_max, index_min, tmp;
static int[] Max = Enumerable.Repeat(int.MinValue, 100001).ToArray<int>();
static int[] Min = Enumerable.Repeat(int.MaxValue, 100001).ToArray<int>();
static BufferedStream bs = new BufferedStream(Console.OpenStandardOutput());
static StreamWriter Speak = new StreamWriter(bs);
static void Main()
{
index_max = 1; index_min = 1;
N = int.Parse(Console.ReadLine());
for(int i = 0; i < N; i++)
{
if (i % 2 == 0) MaxInsert(int.Parse(Console.ReadLine()));
else MinInsert(int.Parse(Console.ReadLine()));
Speak.WriteLine(Max[1]);
}
Speak.Close();
}
static void MaxInsert(int k) // 최대 힙에 값을 추가한다.
{
if(Min[1] < k)
{
Max[index_max] = Min[1];
MaxSortUp();
Min[1] = k;
MinSortDown();
}
else
{
Max[index_max] = k;
MaxSortUp();
}
index_max++;
}
static void MaxSortUp() // 최대 힙을 상향식으로 정렬한다.
{
for(int i = index_max; i > 1; i /= 2)
{
if (Max[i] > Max[i / 2])
{
tmp = Max[i];
Max[i] = Max[i / 2];
Max[i / 2] = tmp;
}
else break;
}
}
static void MaxSortDown() // 최대 힙을 하향식으로 정렬한다.
{
for(int i = 1; i <= index_max;)
{
if (Max[i] < Math.Max(Max[i * 2], Max[i * 2 + 1]))
{
i = Max[i * 2] > Max[i * 2 + 1] ? i * 2 : i * 2 + 1;
tmp = Max[i / 2];
Max[i / 2] = Max[i];
Max[i] = tmp;
}
else break;
}
}
static void MinInsert(int k)
{
if (Max[1] > k)
{
Min[index_min] = Max[1];
MinSortUp();
Max[1] = k;
MaxSortDown();
}
else
{
Min[index_min] = k;
MinSortUp();
}
index_min++;
}
static void MinSortUp()
{
for (int i = index_min; i > 1; i /= 2)
{
if (Min[i] < Min[i / 2])
{
tmp = Min[i];
Min[i] = Min[i / 2];
Min[i / 2] = tmp;
}
else break;
}
}
static void MinSortDown()
{
for(int i = 1; i <= index_min;)
{
if (Min[i] > Math.Min(Min[i * 2], Min[i * 2 + 1]))
{
i = Min[i * 2] < Min[i * 2 + 1] ? i * 2 : i * 2 + 1;
tmp = Min[i / 2];
Min[i / 2] = Min[i];
Min[i] = tmp;
}
else break;
}
}
}우선순위 큐를 이용하면 간단하게 해결되나본데 C#에 우선순위 큐를 제공하는 클래스가 없는 것 같다.
