26087 피보나치와 마지막 수열과 쿼리 (백준, python3)

시간 제한	메모리 제한
1.2초	1024MB

문제

(요약함)

0번 항이 1, 1번항이 1로 시작되는 피보나치 수열을 두고 길이 N의 수열A에 대한 쿼리가 주어진다.

 

수열 A는 초기에 모든 값이 0으로 되어있으며 첫 번째 항을 1번 항, 마지막 항을 N번 항으로 한다.

 

쿼리는 l, r로 N이하인 두 개의 자연수로 주어진다. l은 항상 r이하임이 보장된다.

 

쿼리는 수열 A의 l번 항부터 r번 항을 피보나치 수열의 1번 항부터 r-l+1번 항까지로 바꾸는 작업이다.

 

입력

첫째 줄에는 수열의 크기 N이 주어진다. N은 100만 이하의 자연수이다.

둘째 줄에는 쿼리의 수 Q가 주어진다. Q는 100만 이하의 자연수이다.

셋째 줄 부터 Q줄에 걸친 쿼리가 주어진다.

 

출력

모든 쿼리를 순서대로 적용한 후 수열 A의 모든 항을 공백으로 구분해 출력한다.

각 항의 값은 1e9+7로 나눈 값으로 출력한다.

 

---

풀이

문제를 처음 봤을 때는 l, r 구간에 쿼리를 실행하고 r 이후 구간의 값들을 갱신시켜야 하는 줄 알았는데 그런 건 아니었다. 덕분에 Segment tree with Lazy propagation 공부하러 갔다가 문제 다시 읽고 돌아왔다.

 

피보나치 수열을 l, r 구간에 덮어씌우기만 해주면 되기 때문에 피보나치 수열은 한 번만 구해놓고 갖다 쓰면 끝이다. 사실상 피보나치 수열은 장식일 뿐이고 문제의 핵심은 다른 데 있다. 만약 모든 쿼리에 대해 구간 값 갱신을 매번 실행한다고 해보자. 그러면 시간 복잡도는 O(N*Q)로 시간 내에 문제를 해결할 수 없다. 수열에 쿼리라니 뭔가 세그먼트 트리가 필요해 보이지만(필요한지 아닌지는 모르겠음) 다른 방법으로 쿼리를 압축할 수 있다.

 

l, r 구간에 대한 쿼리가 겹치는 경우를 생각해보자. 아래 그림의 파란색 띠는 쿼리에서 제시한 구간을 나타낸 것이다 .위에서 아래로 쿼리가 입력된다고 해보자.

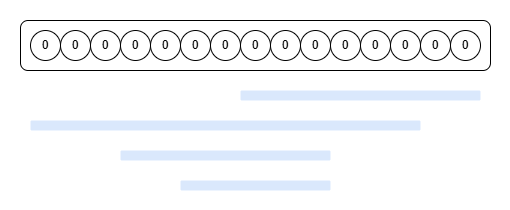
쿼리가 모두 실행 되었을 때 가장 마지막으로 덮인 구간의 값들은 이전에 어떤 값들이 있었는지 알 수가 없다. 그리고 알 필요도 없다. 덮인 구간을 정리해서 빨간색으로 표시해보면 아래와 같다.

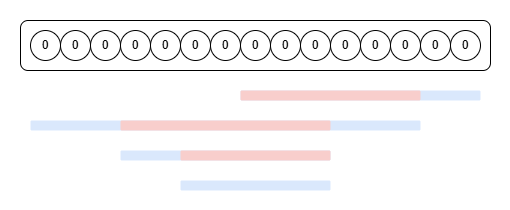
이 구간들은 사실 받지 않아도 되는 정보를 담고 있는 셈이다. 어차피 담아봤자 마지막에 들어온 쿼리에 의해 사라질 것이기 때문이다. 그래서 이 문제는 쿼리를 역순으로 확인하는 것이 효율적이다. 마지막 쿼리부터 확인해 한 번 기록된 구간은 그보다 앞선 쿼리들에 포함된다 해도 처리하지 않는다. 그러면 O(N*Q)에서 일부 쿼리가 생략되어 실행 시간을 줄일 수 있다.

 

이전에 다뤄진 구간은 어떻게 확인할 수 있을까? 수열의 l부터 r까지의 값이 변경되었다면 l부터 r까지의 값들은 모두 r을 구간의 끝으로 한다. 쿼리를 수행할 때마다 수열의 어느 지점이 이미 채워진 상태라면 그게 언제 어느 구간까지 채워졌는지 빠르게 알 수 있고 불필요하게 한 칸씩 넘어가며 빈 칸을 찾을 필요가 없다.

 

30705 ENDLESS RAIN (백준, python3)

이 문제는 이전에 정리했던 문제의 풀이인데 아이디어가 같다. 유니온 파인드를 이용해 이전에 탐색했던 구간의 끝을 빠르게 확인하는 것이 문제 해결의 핵심이다.

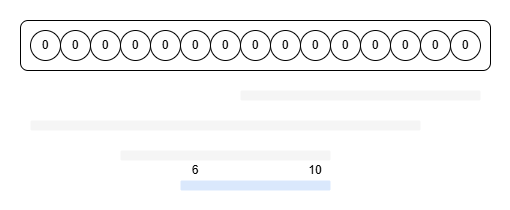
쿼리를 역순으로 처리해야 함은 앞서 설명했으므로 편의상 마지막 쿼리를 첫 번째 쿼리로 바꿔서 부르자. 첫 번째 쿼리가 들어왔다. l부터 r까지 인덱스를 이동하며 확인하되, 수열에 기록된 값이 가리키는 구간 끝을 보면서 인덱스를 건너뛰어주자. 처음엔 수열이 모두 비어있으므로 피보나치 수열이 순차적으로 입력된다. 입력과 동시에 각 칸이 다음 칸을 가리키도록 해준다. 구간의 마지막인 r은 자기 자신을 가리키고 있어야 한다.

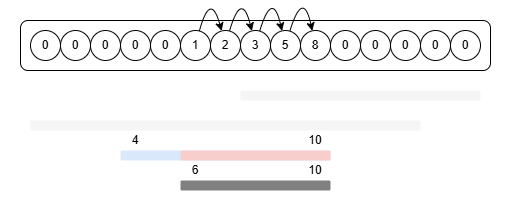
다음 구간은 4에서 10이다. 4, 5까지는 수열에 아무 값도 없으니 피보나치 수열의 값을 입력한다. 5에서 다음 칸으로 넘어갔을 때 6번 값은 이미 채워져 있으므로 확인하지 않고 어디를 가리키는지 살펴본다. 10번 값을 가리키고 있으므로 11번 칸으로 넘어간다. r의 범위를 벗어났으므로 다음 쿼리로 넘어간다.

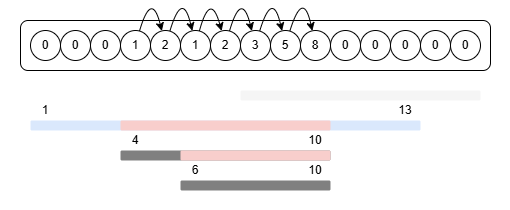
여기서 한 가지 필요한 작업이 더 있는데 6에서 10의 구간을 점프할 때 해당 구간이 가리키는 head를 끝 값으로 갱신시켜주는 것이다. 나중에 head를 탐색할 때 탐색 시간을 줄여준다.

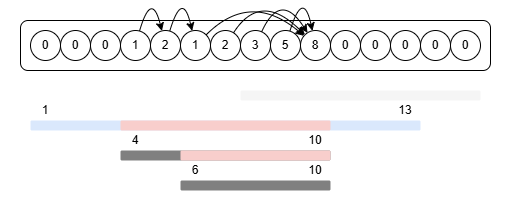
이제 1에서 13이다. 1, 2, 3은 수열이 비었으므로 채워주고, 4에서 5, 5에서 6, 6에서 10을 가리키고 11번 칸을 채워넣게 된다. 역시 마찬가지로 4, 5의 head를 10으로 갱신시켜주면서 11, 12, 13을 마저 채워주면 이번 쿼리도 끝이다.

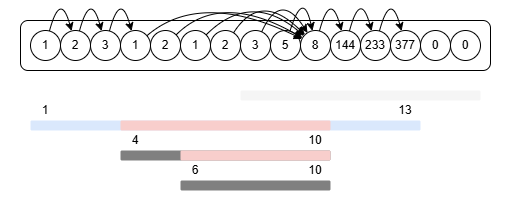
마지막 쿼리도 같은 방법으로 처리할 수 있다. 이렇게 이미 처리된 구간을 유니온 파인드로 건너 뛰게 되면 O(Q*logN)으로 시간 내에 문제를 해결할 수 있다.

 

아니 근데 생각해보니 피보나치 문제도 아니고 낚시성이 너무 강한 문제 아닌가 이거...

 

정답 코드

import sys
input = sys.stdin.readline
def solution():
    N = int(input())
    Q = int(input())
    query = [tuple(map(int, input().split())) for _ in range(Q)]
    fib = [0] * (N + 1)
    fib[0] = 1
    fib[1] = 1
    for i in range(2, N + 1):
        fib[i] = (fib[i - 1] + fib[i - 2]) % 1000000007

    head = [i for i in range(N + 1)]

    def find(k):
        r = k
        while head[r] != r:
            r = head[r]
        while head[k] != k:
            t = head[k]
            head[k] = r
            k = t
        return k

    res = [0] * N
    for l, r in reversed(query):
        l -= 1; r -= 1
        k = l
        while True:
            if res[k] == 0:
                res[k] = fib[k - l + 1]
            k = find(k) + 1
            if k <= r:
                head[k - 1] = k
            else:
                break
    print(*res)
solution()