| 시간 제한 | 메모리 제한 |
| 2초 | 1024MB |
문제
정점이 N개가 있는 트리가 있고 각 정점들은 1부터 N까지 번호가 매겨있다. 해당 트리로부터 (N-2)개의 양의 정수로 이루어진 수열 하나를 다음과 같은 과정을 통해서 만들 것이다.
- 차수가 1인 정점들 중에서 번호가 가장 큰 정점을 하나 고른다. 해당 정점을 x라고 부르자.
- 정점 x와 인접한 정점의 번호를 수열에 넣는다.
- 정점 x와 인접한 간선들을 해당 트리에서 지운다.
- 1번부터 3번까지의 과정을 총 (N - 2)번 진행한다.
수열 {a1, ... , aN-2}가 주어졌을 때, 위의 과정을 통해서 이 수열을 만들 수 있는 트리를 구하여라.
입력
다음과 같이 입력이 주어진다.
N
a1 ··· aN-2
출력
해당 트리가 존재한다면 간선 (N-1) 개를 다음 규칙에 만족하게 출력한다.
- 각 간선은 a b형태로 출력해야 하며 a < b를 만족하여야 한다.
- 간선을 사전 순으로 출력해야 한다. 즉, 임의의 두 간선 (a1, b1)과 (a2, b2)에 대해 a1 < a2를 만족하거나 a1 = a2, b1 < b2를 만족하는 경우 (a1, b1) 간선을 (a2, b2) 간선보다 먼저 출력해야 한다.
만약 트리가 존재하지 않거나 2개 이상 존재하는 경우에는 -1을 출력하여라.
풀이
접근 방법을 찾아보기 위해 먼저 수열과 트리 사이의 관계를 이해해봅시다. 예제 출력 1의 트리를 그려보고, 이 트리로부터 예제 입력 1의 수열을 얻어봅시다.
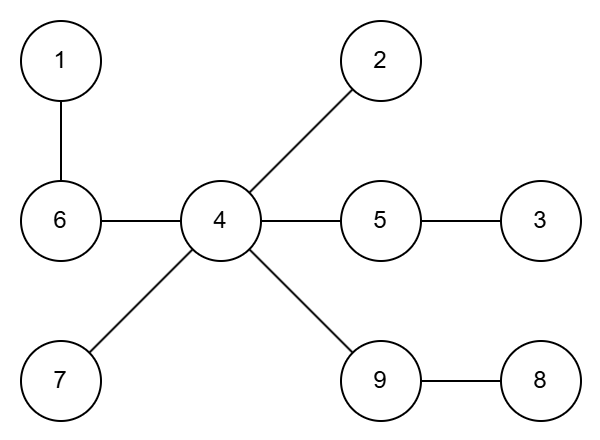
규칙에 따르면 차수, 그러니까 연결된 간선의 수가 1개뿐인 정점 중 번호가 가장 큰 것을 고릅니다. 차수가 1인 정점이란 리프 노드를 의미합니다.
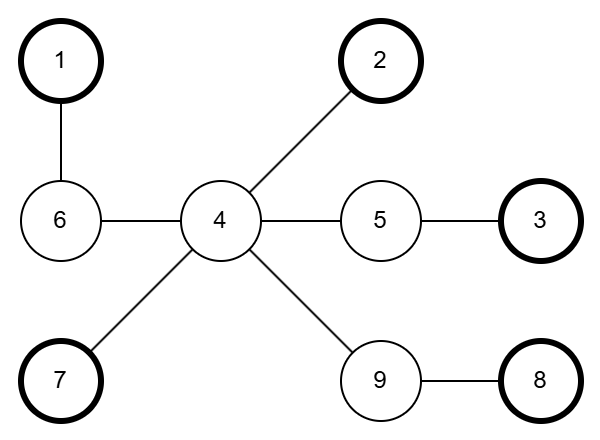
리프인 1, 2, 3, 7, 8 중 가장 큰 수는 8입니다. 8을 제거하고 8과 연결되어있는 정점 9를 수열에 추가합니다. 그리고 8-9 간선을 삭제합니다.
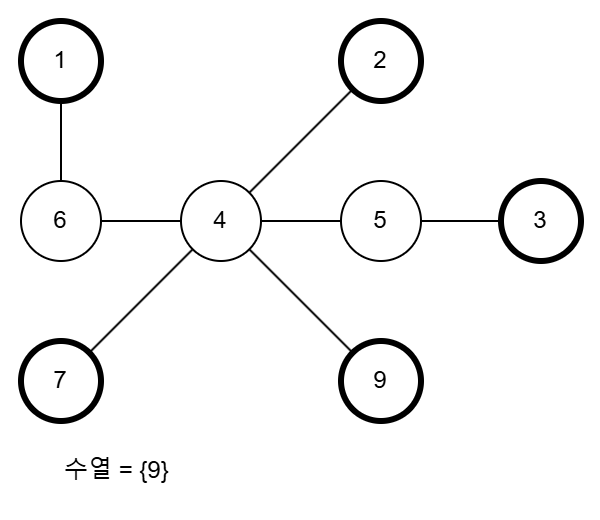
이제 리프는 1, 2, 3, 7, 9가 되었습니다. 이번에는 9가 삭제되고, 수열에 4가 추가됩니다. 과정을 3회 진행시켜보겠습니다. 다음으로는 7이, 그 다음은 3이 삭제됩니다.
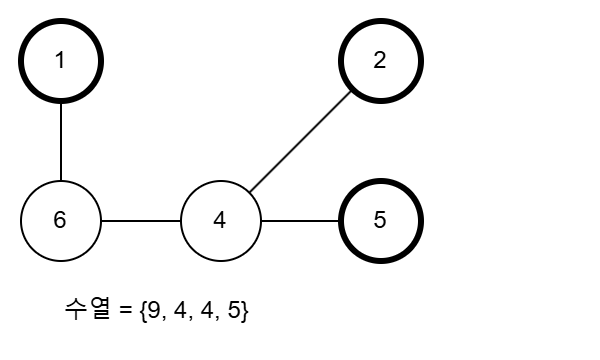
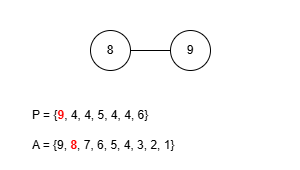
이렇게 과정을 끝까지 진행시키면 5, 2, 4가 순서대로 더 제거되며 수열은 {9, 4, 4, 5, 4, 4, 6}이 되고, 1-6만이 트리에 남게 됩니다. 이 과정을 거쳐서 트리를 수열로 변환시킬 수 있습니다. 이 과정과 관련이 있는 개념이 하나 있습니다.
Prüfer sequence - Wikipedia
From Wikipedia, the free encyclopedia Mathematical sequence In combinatorial mathematics, the Prüfer sequence (also Prüfer code or Prüfer numbers) of a labeled tree is a unique sequence associated with the tree. The sequence for a tree on n vertices has
en.wikipedia.org
문제와 달리 프뤼퍼 수열은 리프 노드 중 번호가 가장 작은 것을 제거합니다. 이 부분은 나중에 살펴보겠습니다. 그리고 프뤼퍼 수열의 중요한 특징이 하나 있습니다. 문제의 출력 조건 마지막 줄에는 주어진 수열로 트리가 구성되지 않거나 2개 이상의 트리가 존재하게 되는 경우는 -1을 출력하라고 했습니다. 하지만 프뤼퍼 수열 P = {a1, a2, ..., aN-2}에서 1 ≤ ai ≤ N - 2가 보장되는 경우, 반드시 대응하는 트리가 유일하게 존재하는 것이 증명되어 있습니다. 따라서 N개의 정점으로 만들어지는 프뤼퍼 수열은 NN-2이며, N개의 정점으로 만들 수 있는 트리의 수와 같습니다.(Cayley's formula)
그렇다면 어떤 트리에 대해 유일하게 대응되는 프뤼퍼 수열을 원래의 트리로 변환하는 방법을 알아봅시다.
Labeled Tree from Prüfer Sequence - ProofWiki
Algorithm Given a Prüfer sequence, it is possible to generate a finite labeled tree corresponding to that sequence. Let $P = \tuple {\mathbf a_1, \mathbf a_2, \ldots, \mathbf a_{n - 2} }$ be a Prüfer sequence. This will be called the sequence. It is assu
proofwiki.org
프뤼퍼 수열 P = {a1, a2, ..., aN-2}에서 트리를 구성하는 과정은 다음과 같습니다.
- 먼저 N개의 노드를 그립니다. 각 노드는 1부터 N까지의 번호를 부여 받고 서로 연결되어있지 않습니다.
- 1부터 N까지의 정수를 순서대로 나열한 배열 A를 생성합니다.
- 만약 A에 남은 값이 2개라면 그 두 값을 연결하고 마칩니다. 아니라면 다음 단계로 넘어갑니다.
- P에 포함되지 않은 가장 작은 A의 원소를 찾아 P의 맨 앞 원소와 연결합니다.
- 연결한 두 원소를 각각 A와 P에서 삭제하고 3으로 돌아갑니다.
이 규칙에 따라 앞서 예제로 사용한 수열 P = {9, 4, 4, 5, 4, 4, 6}을 트리로 복원해봅시다. 그런데 이 문제에선 프뤼퍼 수열을 구성할 때 리프 중 가장 큰 값을 먼저 삭제했기 때문에 복원을 위한 배열 A를 역순으로 구성해야 합니다.
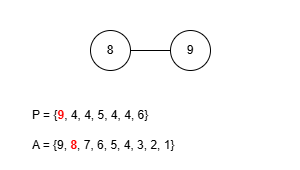
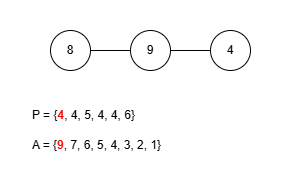
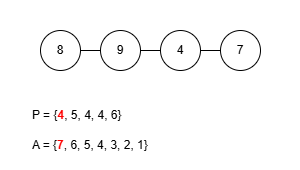
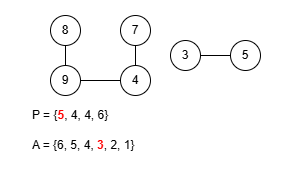
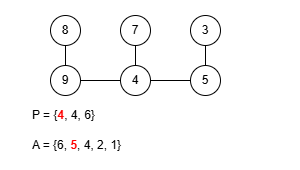
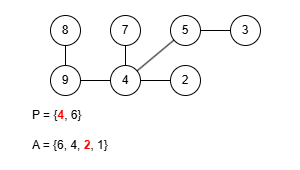
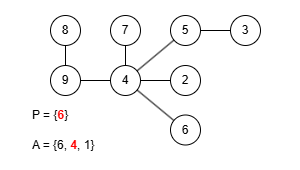
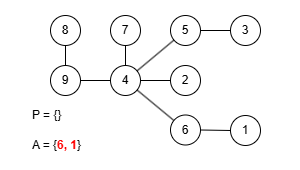
완성된 트리는 예제 출력에 있는 것과 같습니다. 정상적으로 트리를 구성하는 데 성공했으니 이제 이걸 코드로 작성해봅시다. 먼저 정점의 수는 최대 50만개 입니다. 여기서 배열 A를 관리하는 과정을 생각해보면 P에 포함되지 않은 가장 큰 값을 꺼내야 하는데 꺼낸 후에는 그 값이 삭제되어야 합니다. 만약 매번 배열에서 직접 값을 삭제시키고 재정렬한다면 O(N2)의 시간복잡도로 시간 제한 내에 문제를 해결할 수 없습니다. 다른 방법을 생각해봅시다.
먼저 저는 A에서 삭제된 값들을 유니온 파인드로 관리해보기로 했습니다. 삭제된 값들이 다음 값들을 head로 가리키고 root에는 배열의 오른쪽 방향으로 가장 가까운 삭제되지 않은 값이 나타난다면 보다 빠르게 다음 값을 꺼내올 수 있습니다. 여기서 각 시도에 소모되는 시간은 평균 O(logN)이지만 배열의 특성상 맨 끝 값부터 빠져나간다고 한다면(최악의 경우) 아무 의미가 없고 여전히 O(N2)의 시간복잡도를 갖습니다. 따라서 유니온파인드로는 이 문제의 조건을 만족할 수 없습니다.
맨 끝 값부터 계속 꺼내오는 최악의 경우에도 O(logN)을 유지하는 다른 방법은 우선순위 큐가 있습니다. 따라서 배열 A를 우선순위 큐로 각 값을 음수로 관리하면 가장 큰 값부터 O(NlogN)으로 모두 꺼내올 수 있습니다.
꺼내온 A의 값 a를 P의 맨 앞 값 p와 비교해 더 작은 값이 앞으로 오도록 (a, p) 또는 (p, a)를 튜플로 저장했습니다. 마지막으로 트리의 연결 구조를 정렬해 출력하면 끝입니다. 주의할 부분은 마지막으로 A에 남은 두 값을 연결하는 건 따로 처리해야 합니다.
정답 코드
import sys
from collections import deque
from heapq import heappush, heappop
input = sys.stdin.readline
def solution():
n = int(input())
count = [0] * (n + 1)
P = deque(list(map(int, input().split())))
for p in P: count[p] += 1
tree = []
L = []
for i in range(1, n + 1):
if count[i] == 0: heappush(L, -i)
for _ in range(n - 2):
l = -heappop(L)
if P[0] > l:
tree.append((l, P[0]))
else:
tree.append((P[0], l))
count[P[0]] -= 1
if count[P[0]] == 0:
heappush(L, -P[0])
P.popleft()
tree.append((-L[1], -L[0]))
tree.sort()
for e in tree:
print(*e)
solution()
| 시간 제한 | 메모리 제한 |
| 2초 | 1024MB |
문제
정점이 N개가 있는 트리가 있고 각 정점들은 1부터 N까지 번호가 매겨있다. 해당 트리로부터 (N-2)개의 양의 정수로 이루어진 수열 하나를 다음과 같은 과정을 통해서 만들 것이다.
- 차수가 1인 정점들 중에서 번호가 가장 큰 정점을 하나 고른다. 해당 정점을 x라고 부르자.
- 정점 x와 인접한 정점의 번호를 수열에 넣는다.
- 정점 x와 인접한 간선들을 해당 트리에서 지운다.
- 1번부터 3번까지의 과정을 총 (N - 2)번 진행한다.
수열 {a1, ... , aN-2}가 주어졌을 때, 위의 과정을 통해서 이 수열을 만들 수 있는 트리를 구하여라.

입력
다음과 같이 입력이 주어진다.
N
a1 ··· aN-2
출력
해당 트리가 존재한다면 간선 (N-1) 개를 다음 규칙에 만족하게 출력한다.
- 각 간선은 a b형태로 출력해야 하며 a < b를 만족하여야 한다.
- 간선을 사전 순으로 출력해야 한다. 즉, 임의의 두 간선 (a1, b1)과 (a2, b2)에 대해 a1 < a2를 만족하거나 a1 = a2, b1 < b2를 만족하는 경우 (a1, b1) 간선을 (a2, b2) 간선보다 먼저 출력해야 한다.
만약 트리가 존재하지 않거나 2개 이상 존재하는 경우에는 -1을 출력하여라.
풀이
접근 방법을 찾아보기 위해 먼저 수열과 트리 사이의 관계를 이해해봅시다. 예제 출력 1의 트리를 그려보고, 이 트리로부터 예제 입력 1의 수열을 얻어봅시다.

규칙에 따르면 차수, 그러니까 연결된 간선의 수가 1개뿐인 정점 중 번호가 가장 큰 것을 고릅니다. 차수가 1인 정점이란 리프 노드를 의미합니다.

리프인 1, 2, 3, 7, 8 중 가장 큰 수는 8입니다. 8을 제거하고 8과 연결되어있는 정점 9를 수열에 추가합니다. 그리고 8-9 간선을 삭제합니다.

이제 리프는 1, 2, 3, 7, 9가 되었습니다. 이번에는 9가 삭제되고, 수열에 4가 추가됩니다. 과정을 3회 진행시켜보겠습니다. 다음으로는 7이, 그 다음은 3이 삭제됩니다.

이렇게 과정을 끝까지 진행시키면 5, 2, 4가 순서대로 더 제거되며 수열은 {9, 4, 4, 5, 4, 4, 6}이 되고, 1-6만이 트리에 남게 됩니다. 이 과정을 거쳐서 트리를 수열로 변환시킬 수 있습니다. 이 과정과 관련이 있는 개념이 하나 있습니다.
Prüfer sequence - Wikipedia
From Wikipedia, the free encyclopedia Mathematical sequence In combinatorial mathematics, the Prüfer sequence (also Prüfer code or Prüfer numbers) of a labeled tree is a unique sequence associated with the tree. The sequence for a tree on n vertices has
en.wikipedia.org
문제와 달리 프뤼퍼 수열은 리프 노드 중 번호가 가장 작은 것을 제거합니다. 이 부분은 나중에 살펴보겠습니다. 그리고 프뤼퍼 수열의 중요한 특징이 하나 있습니다. 문제의 출력 조건 마지막 줄에는 주어진 수열로 트리가 구성되지 않거나 2개 이상의 트리가 존재하게 되는 경우는 -1을 출력하라고 했습니다. 하지만 프뤼퍼 수열 P = {a1, a2, ..., aN-2}에서 1 ≤ ai ≤ N - 2가 보장되는 경우, 반드시 대응하는 트리가 유일하게 존재하는 것이 증명되어 있습니다. 따라서 N개의 정점으로 만들어지는 프뤼퍼 수열은 NN-2이며, N개의 정점으로 만들 수 있는 트리의 수와 같습니다.(Cayley's formula)
그렇다면 어떤 트리에 대해 유일하게 대응되는 프뤼퍼 수열을 원래의 트리로 변환하는 방법을 알아봅시다.
Labeled Tree from Prüfer Sequence - ProofWiki
Algorithm Given a Prüfer sequence, it is possible to generate a finite labeled tree corresponding to that sequence. Let $P = \tuple {\mathbf a_1, \mathbf a_2, \ldots, \mathbf a_{n - 2} }$ be a Prüfer sequence. This will be called the sequence. It is assu
proofwiki.org
프뤼퍼 수열 P = {a1, a2, ..., aN-2}에서 트리를 구성하는 과정은 다음과 같습니다.
- 먼저 N개의 노드를 그립니다. 각 노드는 1부터 N까지의 번호를 부여 받고 서로 연결되어있지 않습니다.
- 1부터 N까지의 정수를 순서대로 나열한 배열 A를 생성합니다.
- 만약 A에 남은 값이 2개라면 그 두 값을 연결하고 마칩니다. 아니라면 다음 단계로 넘어갑니다.
- P에 포함되지 않은 가장 작은 A의 원소를 찾아 P의 맨 앞 원소와 연결합니다.
- 연결한 두 원소를 각각 A와 P에서 삭제하고 3으로 돌아갑니다.
이 규칙에 따라 앞서 예제로 사용한 수열 P = {9, 4, 4, 5, 4, 4, 6}을 트리로 복원해봅시다. 그런데 이 문제에선 프뤼퍼 수열을 구성할 때 리프 중 가장 큰 값을 먼저 삭제했기 때문에 복원을 위한 배열 A를 역순으로 구성해야 합니다.








완성된 트리는 예제 출력에 있는 것과 같습니다. 정상적으로 트리를 구성하는 데 성공했으니 이제 이걸 코드로 작성해봅시다. 먼저 정점의 수는 최대 50만개 입니다. 여기서 배열 A를 관리하는 과정을 생각해보면 P에 포함되지 않은 가장 큰 값을 꺼내야 하는데 꺼낸 후에는 그 값이 삭제되어야 합니다. 만약 매번 배열에서 직접 값을 삭제시키고 재정렬한다면 O(N2)의 시간복잡도로 시간 제한 내에 문제를 해결할 수 없습니다. 다른 방법을 생각해봅시다.
먼저 저는 A에서 삭제된 값들을 유니온 파인드로 관리해보기로 했습니다. 삭제된 값들이 다음 값들을 head로 가리키고 root에는 배열의 오른쪽 방향으로 가장 가까운 삭제되지 않은 값이 나타난다면 보다 빠르게 다음 값을 꺼내올 수 있습니다. 여기서 각 시도에 소모되는 시간은 평균 O(logN)이지만 배열의 특성상 맨 끝 값부터 빠져나간다고 한다면(최악의 경우) 아무 의미가 없고 여전히 O(N2)의 시간복잡도를 갖습니다. 따라서 유니온파인드로는 이 문제의 조건을 만족할 수 없습니다.
맨 끝 값부터 계속 꺼내오는 최악의 경우에도 O(logN)을 유지하는 다른 방법은 우선순위 큐가 있습니다. 따라서 배열 A를 우선순위 큐로 각 값을 음수로 관리하면 가장 큰 값부터 O(NlogN)으로 모두 꺼내올 수 있습니다.
꺼내온 A의 값 a를 P의 맨 앞 값 p와 비교해 더 작은 값이 앞으로 오도록 (a, p) 또는 (p, a)를 튜플로 저장했습니다. 마지막으로 트리의 연결 구조를 정렬해 출력하면 끝입니다. 주의할 부분은 마지막으로 A에 남은 두 값을 연결하는 건 따로 처리해야 합니다.
정답 코드
import sys
from collections import deque
from heapq import heappush, heappop
input = sys.stdin.readline
def solution():
n = int(input())
count = [0] * (n + 1)
P = deque(list(map(int, input().split())))
for p in P: count[p] += 1
tree = []
L = []
for i in range(1, n + 1):
if count[i] == 0: heappush(L, -i)
for _ in range(n - 2):
l = -heappop(L)
if P[0] > l:
tree.append((l, P[0]))
else:
tree.append((P[0], l))
count[P[0]] -= 1
if count[P[0]] == 0:
heappush(L, -P[0])
P.popleft()
tree.append((-L[1], -L[0]))
tree.sort()
for e in tree:
print(*e)
solution()
