https://www.acmicpc.net/problem/16877
| 시간 제한 | 메모리 제한 |
| 0.5초 | 512MB |
문제
koosaga와 cubelover가 "핌버"를 하고 있다. 핌버는 님 게임에 규칙을 추가한 게임이다. 핌버는 돌을 차곡 차곡 위로 쌓아올린 돌 더미 k개를 이용한다. 각각의 돌 더미에는 한 개 이상의 돌이 있다. 두 사람은 서로 턴을 번갈아가면서 핌버를 진행한다. 각 사람의 턴이 되면, 돌 더미 하나를 선택해 돌을 제거한다. 제거한 돌의 개수는 피보나치 수여야 한다.
전체 돌 더미에서 마지막 돌을 제거하는 사람이 게임을 이기게 된다.
게임은 koosaga가 먼저 시작한다. 두 사람이 최적의 방법으로 게임을 진행했을 때, 이기는 사람을 출력한다.
입력
첫째 줄에 돌 더미의 개수 N (1 ≤ N ≤ 105)이 주어진다. 둘째 줄에 각 돌 더미에 쌓여있는 돌의 개수 Pi (1 ≤ Pi ≤ 3×106)가 주어진다.
출력
koosaga가 이기는 경우에는 "koosaga"를, cubelover가 이기는 경우에는 "cubelover"를 출력한다.
풀이
nim게임의 변형 문제입니다. 우선 일반적인 nim게임은 동적계획법으로 승패 여부를 판단하는 것이 가능하지만 이 문제에서는 "피보나치 수"이기만 하면 몇 개의 돌을 제거하든 상관이 없습니다. 자기 차례에 할 수 있는 행동의 가짓수가 너무 많기 때문에 일반적인 nim게임 풀이법으로는 해결이 어렵습니다.
님 (게임) - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전.
ko.wikipedia.org
여기서 "조합론적 게임 이론"이 필요합니다. nim게임의 상위 호환인 분류인데, 다음과 같은 조건이 붙습니다.
- 두 플레이어가 번갈아가며 행동한다.
- 플레이어는 게임 내의 모든 정보를 공유하고 알고 있다.
- 자신의 차례가 되었을 때 할 수 있는 행동이 없으면 패배한다.
이런 게임들의 특징은 게임 중 발생한 어떤 상태가 다른 상태와 연결관계를 갖습니다. 틱택토를 예로 보겠습니다.
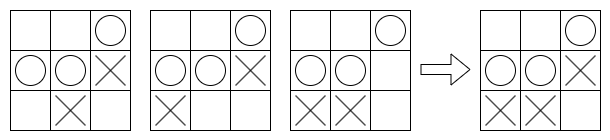
오른쪽 상태는 왼쪽 상태로부터 이어집니다. 이런 식으로 조합론적 게임에서는 모든 상태가 서로 이어지며 최초 상태와 이어지지 않는 상태는 어떤 방법으로 게임을 진행해도 만들어질 수 없습니다. 그리고 각각의 상태는 모두 최종 상태(승리)로 이어질 수 있습니다. 승리 상태로만 이어지는 이유는 플레이어 기준으로 보는 것이 아니라 게임 상태를 기준으로 보기 때문입니다. 게임은 누군가 승리 상태를 만들면 끝납니다.
이제 각 상태를 구분할 수 있는 값을 매겨봅시다.(저는 이 과정이 해싱과 비슷하다는 느낌을 받았습니다.) 게임 중 어떤 상태 n에 대한 값을 G(n)라고 합니다. 이걸 "Grundy number(그런디 수)"라고 부릅니다. 먼저, 아무 행동도 할 수 없는 상태(승리)의 그런디 수를 0으로 정합니다. 그리고 그 이전 상태의 그런디 수를 정할 수 있습니다. 이때 필요한 함수를 mex(Max EXcluded number)라고 합니다. mex는 현재 상태에서 연결되는 다음 상태의 모든 그런디 수가 아닌 0 이상의 가장 작은 정수입니다. 뭔가 복잡한데 이런 식입니다. 대표적인 조합론적 게임 "배스킨라빈스31"을 예로 들어봅시다. 이 게임에서는 최소 1개, 최대 3개의 숫자를 연속해서 말할 수 있고, 31을 말하는 사람이 패배합니다. 그러니까 31을 말할 수 밖에 없는 상태를 만들면 승리합니다.

30을 말하게 되면 이어지는 다음 상태가 존재하지 않습니다. 따라서 이어지는 G(n) 집합은 공집합이고 이때 mex는 G(30) = 0이 됩니다. 29를 말하게 되면 이어지는 상태는 30까지 말하는 경우 뿐입니다. 이어지는 G(n) 집합은 {G(30)} = {0}이므로 mex는 G(29) = 1이 됩니다. 26의 경우는 이어지는 상태가 27, 28, 29이며 각각 그런디 수가 3, 2, 1입니다. 26에 대한 mex는 0입니다. 따라서 G(26) = 0입니다. 이와 같이 그런디 수를 파악해 G(n) = 0이 되는 상태가 반드시 승리할 수 있는 상태가 됩니다. 이제 그런디 수를 이용해 독립된 조합론적 게임을 여러 번 수행할 때 반드시 이길 수 있는지 확인하는 "Sprague-Grundy Theorem(스프라그-그런디 정리)"를 이용해봅시다.
Sprague–Grundy theorem - Wikipedia
From Wikipedia, the free encyclopedia Every impartial game position is equivalent to a position in the game of nim In combinatorial game theory, the Sprague–Grundy theorem states that every impartial game under the normal play convention is equivalent to
en.wikipedia.org
자세한 내용은 위키를 봅시다.(굳이 다 이해할 필요는 없을 것 같아서 저도 안 읽었어요.)
스프라그-그런디 정리에 따르면 여러 개의 조합론적 게임의 그런디 수를 모두 xor 합한 결과가 0이라면 전체 게임을 모두 최선의 수를 두어 진행했을 때 최종 승리할 수 있고, 0이 아니라면 최종 승리할 수 없다고 합니다.
그럼 이제 주어진 문제에서 각각의 돌 더미에 대한 그런디 수를 구해야 합니다. 여기서 돌 무더기마다 돌의 수는 10만 개입니다. 10만 개의 그런디 수를 구하는 건 그리 어렵지 않아보입니다. 문제는 mex를 구하는 과정입니다. "제거할 수 있는 돌의 수가 피보나치 수이기만 하면 된다"는 조건 때문에 이어지는 상태가 매우 많아지기 때문입니다. 여기서 이어지는 상태의 그런디 수를 파악해 mex를 빠르게 찾을 방법을 생각해봅시다.
이 문제에서 존재하는 가장 큰 그런디 수는 15입니다. 매 탐색마다 16크기의 bool 타입 배열을 만들어 존재하는 그런디 수를 True로 바꿔주면 가장 앞선 False의 인덱스가 mex가 됩니다.
정답 코드
import sys
input = sys.stdin.readline
def solution():
fib = [1] * 32
grundy = [0] * 3000001
for i in range(2, 32):
fib[i] = fib[i - 1] + fib[i - 2]
for i in range(1, 3000001):
states = [0] * 16
for f in fib:
if f > i: break
states[grundy[i - f]] = 1
for g in range(16):
if states[g] == 0:
grundy[i] = g
break
n = int(input())
p = list(map(int, input().split()))
res = grundy[p[0]]
for i in range(1, n):
res ^= grundy[p[i]]
print("koosaga" if res else "cubelover")
solution()
https://www.acmicpc.net/problem/16877
| 시간 제한 | 메모리 제한 |
| 0.5초 | 512MB |
문제
koosaga와 cubelover가 "핌버"를 하고 있다. 핌버는 님 게임에 규칙을 추가한 게임이다. 핌버는 돌을 차곡 차곡 위로 쌓아올린 돌 더미 k개를 이용한다. 각각의 돌 더미에는 한 개 이상의 돌이 있다. 두 사람은 서로 턴을 번갈아가면서 핌버를 진행한다. 각 사람의 턴이 되면, 돌 더미 하나를 선택해 돌을 제거한다. 제거한 돌의 개수는 피보나치 수여야 한다.
전체 돌 더미에서 마지막 돌을 제거하는 사람이 게임을 이기게 된다.
게임은 koosaga가 먼저 시작한다. 두 사람이 최적의 방법으로 게임을 진행했을 때, 이기는 사람을 출력한다.
입력
첫째 줄에 돌 더미의 개수 N (1 ≤ N ≤ 105)이 주어진다. 둘째 줄에 각 돌 더미에 쌓여있는 돌의 개수 Pi (1 ≤ Pi ≤ 3×106)가 주어진다.
출력
koosaga가 이기는 경우에는 "koosaga"를, cubelover가 이기는 경우에는 "cubelover"를 출력한다.
풀이
nim게임의 변형 문제입니다. 우선 일반적인 nim게임은 동적계획법으로 승패 여부를 판단하는 것이 가능하지만 이 문제에서는 "피보나치 수"이기만 하면 몇 개의 돌을 제거하든 상관이 없습니다. 자기 차례에 할 수 있는 행동의 가짓수가 너무 많기 때문에 일반적인 nim게임 풀이법으로는 해결이 어렵습니다.
님 (게임) - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전.
ko.wikipedia.org
여기서 "조합론적 게임 이론"이 필요합니다. nim게임의 상위 호환인 분류인데, 다음과 같은 조건이 붙습니다.
- 두 플레이어가 번갈아가며 행동한다.
- 플레이어는 게임 내의 모든 정보를 공유하고 알고 있다.
- 자신의 차례가 되었을 때 할 수 있는 행동이 없으면 패배한다.
이런 게임들의 특징은 게임 중 발생한 어떤 상태가 다른 상태와 연결관계를 갖습니다. 틱택토를 예로 보겠습니다.

오른쪽 상태는 왼쪽 상태로부터 이어집니다. 이런 식으로 조합론적 게임에서는 모든 상태가 서로 이어지며 최초 상태와 이어지지 않는 상태는 어떤 방법으로 게임을 진행해도 만들어질 수 없습니다. 그리고 각각의 상태는 모두 최종 상태(승리)로 이어질 수 있습니다. 승리 상태로만 이어지는 이유는 플레이어 기준으로 보는 것이 아니라 게임 상태를 기준으로 보기 때문입니다. 게임은 누군가 승리 상태를 만들면 끝납니다.
이제 각 상태를 구분할 수 있는 값을 매겨봅시다.(저는 이 과정이 해싱과 비슷하다는 느낌을 받았습니다.) 게임 중 어떤 상태 n에 대한 값을 G(n)라고 합니다. 이걸 "Grundy number(그런디 수)"라고 부릅니다. 먼저, 아무 행동도 할 수 없는 상태(승리)의 그런디 수를 0으로 정합니다. 그리고 그 이전 상태의 그런디 수를 정할 수 있습니다. 이때 필요한 함수를 mex(Max EXcluded number)라고 합니다. mex는 현재 상태에서 연결되는 다음 상태의 모든 그런디 수가 아닌 0 이상의 가장 작은 정수입니다. 뭔가 복잡한데 이런 식입니다. 대표적인 조합론적 게임 "배스킨라빈스31"을 예로 들어봅시다. 이 게임에서는 최소 1개, 최대 3개의 숫자를 연속해서 말할 수 있고, 31을 말하는 사람이 패배합니다. 그러니까 31을 말할 수 밖에 없는 상태를 만들면 승리합니다.

30을 말하게 되면 이어지는 다음 상태가 존재하지 않습니다. 따라서 이어지는 G(n) 집합은 공집합이고 이때 mex는 G(30) = 0이 됩니다. 29를 말하게 되면 이어지는 상태는 30까지 말하는 경우 뿐입니다. 이어지는 G(n) 집합은 {G(30)} = {0}이므로 mex는 G(29) = 1이 됩니다. 26의 경우는 이어지는 상태가 27, 28, 29이며 각각 그런디 수가 3, 2, 1입니다. 26에 대한 mex는 0입니다. 따라서 G(26) = 0입니다. 이와 같이 그런디 수를 파악해 G(n) = 0이 되는 상태가 반드시 승리할 수 있는 상태가 됩니다. 이제 그런디 수를 이용해 독립된 조합론적 게임을 여러 번 수행할 때 반드시 이길 수 있는지 확인하는 "Sprague-Grundy Theorem(스프라그-그런디 정리)"를 이용해봅시다.
Sprague–Grundy theorem - Wikipedia
From Wikipedia, the free encyclopedia Every impartial game position is equivalent to a position in the game of nim In combinatorial game theory, the Sprague–Grundy theorem states that every impartial game under the normal play convention is equivalent to
en.wikipedia.org
자세한 내용은 위키를 봅시다.(굳이 다 이해할 필요는 없을 것 같아서 저도 안 읽었어요.)
스프라그-그런디 정리에 따르면 여러 개의 조합론적 게임의 그런디 수를 모두 xor 합한 결과가 0이라면 전체 게임을 모두 최선의 수를 두어 진행했을 때 최종 승리할 수 있고, 0이 아니라면 최종 승리할 수 없다고 합니다.
그럼 이제 주어진 문제에서 각각의 돌 더미에 대한 그런디 수를 구해야 합니다. 여기서 돌 무더기마다 돌의 수는 10만 개입니다. 10만 개의 그런디 수를 구하는 건 그리 어렵지 않아보입니다. 문제는 mex를 구하는 과정입니다. "제거할 수 있는 돌의 수가 피보나치 수이기만 하면 된다"는 조건 때문에 이어지는 상태가 매우 많아지기 때문입니다. 여기서 이어지는 상태의 그런디 수를 파악해 mex를 빠르게 찾을 방법을 생각해봅시다.
이 문제에서 존재하는 가장 큰 그런디 수는 15입니다. 매 탐색마다 16크기의 bool 타입 배열을 만들어 존재하는 그런디 수를 True로 바꿔주면 가장 앞선 False의 인덱스가 mex가 됩니다.
정답 코드
import sys
input = sys.stdin.readline
def solution():
fib = [1] * 32
grundy = [0] * 3000001
for i in range(2, 32):
fib[i] = fib[i - 1] + fib[i - 2]
for i in range(1, 3000001):
states = [0] * 16
for f in fib:
if f > i: break
states[grundy[i - f]] = 1
for g in range(16):
if states[g] == 0:
grundy[i] = g
break
n = int(input())
p = list(map(int, input().split()))
res = grundy[p[0]]
for i in range(1, n):
res ^= grundy[p[i]]
print("koosaga" if res else "cubelover")
solution()
