14601 샤워실 바닥 깔기 (Large) (백준, python3)

https://www.acmicpc.net/problem/14601

시간 제한	메모리 제한
1초	512MB

문제

오늘은 민규가 훈련소에 입소하는 날이다. 모든 행사를 마치고 생활관으로 돌아와서 쉬려는데 갑자기 교관이 들어오더니 민규의 이름을 부르는 것이 아닌가. 당황한 채로 따라갔더니 이번엔 김준서를 아느냐고 물어보았다. 그 녀석이 샤워실 바닥을 깔았는데, 배수구 위치까지 막아버렸다면서 같은 학교 출신인 민규가 다시 깔라는 것이었다.

어떻게 타일을 깔지 고민하던 민규는 샤워실의 구조가 정사각형이면서 한 변의 길이가 2의 제곱수라는 사실을 알아냈다. 준서는 여기까지만 고려해서 2x2 크기의 타일로 바닥을 전부 채운 것 같은데, 문제는 이렇게 하면 배수구가 있어야 할 위치를 비울 수가 없다는 것이다. 이런저런 방법을 생각하다가 4칸을 차지하는 정사각형 타일 대신 3칸을 차지하는 ㄱ자 모양의 타일을 사용하면 될 것 같다는 느낌을 받았다.

그런데 ㄱ자 타일을 어떻게 채워야 할까? 생각하다 지친 민규는 여러분에게 이 방법을 찾아달라고 부탁했다. 첫날부터 생활관에서 밤을 새우는 일이 없도록 여러분이 도와주자.

 

입력

첫 번째 줄에는 바닥의 한 변의 길이를 표현하는 자연수 K(1 ≤ K ≤ 7) 가 주어진다. 이때 바닥의 크기는 2^K 가 됨에 유의하라. 두 번째 줄에는 배수구의 위치를 나타내는 자연수 x, y (1 ≤ x, y ≤ 2^K)가 공백으로 분리돼서 주어진다. 이때 가장 왼쪽 아래가 (1, 1), 가장 오른쪽 위가 (2^K, 2^K)이다.

 

출력

각 타일마다 고유한 번호를 매긴 타일의 배치도를 출력한다. 각 타일의 번호에는 19000 이하의 자연수만을 사용해야 한다. 배수구가 있는 위치는 -1로 표시한다. 가능한 답 중 하나만 출력하면 된다.

만약 알맞게 타일을 배치하는 방법이 존재하지 않는다면 -1을 출력한다.

 

 

풀이

규칙을 찾기 위해 타일을 좀 배치해봅시다.

K가 1일 때는 1개의 타일로 배치가 끝납니다.

K가 2일 때에도 배치가 잘 되는 것 같습니다. x가 어디에 있든 x를 품고 있는 타일이 회전하면 모든 경우를 완성할 수 있습니다.

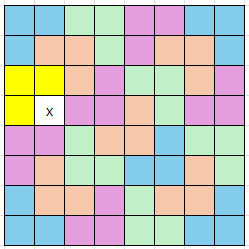
K가 3일 때도 문제 없어보입니다. 이쯤 해보면 규칙이 보입니다.

긴 변의 크기가 2의 거듭제곱이고 단위타일과 닮은 타일이 있다고 해봅시다. 처음에는 2^K와 같은 크기로 배수구가 막하지 않도록 타일을 배치, 그 다음에는 점차 타일의 길이비를 반감시키며 배수구가 막히지 않도록 배치합니다. 그리고 전체 타일을 단위 타일로 쪼개보면 배치가 역시 규칙적입니다. 재귀를 활용한 분할 정복을 하면 딱 좋을 것 같습니다.

 

구현 방법은 여러 가지가 있을 것 같지만 저는 큰 타일부터 순차적으로 까는 방법을 선택했습니다.

 

K = 4인 경우입니다. 먼저 가장 큰 타일을 깔아봅니다.

타일의 안쪽 꼭지점의 단위 타일은 방향이 정해졌습니다. 다음 단계로 들어가봅시다.

길이비를 반감시킨 타일로 분열시켰습니다. 역시 안쪽 꼭지점의 단위 타일은 방향이 정해집니다.

다시 분열된 타일들의 안쪽 꼭지점이 정해집니다. 타일들의 방향은 이전 단계의 타일과의 위치관계로 정해집니다. 이런 방식으로 배수구를 덮지 않는 2^K크기의 타일을 완성합니다. 이제 2^(K-1)크기의 타일을 나머지 빈칸에 같은 방법으로 채워 나갑니다. 타일의 크기가 2가 될 때까지 작업을 반복합니다.

 

 

정답 코드

import sys
input = sys.stdin.readline
def solution():
    k = 1 << int(input())
    floor = [[0] * k for _ in range(k)]
    check = [[0] * k for _ in range(k)]
    idx = [1]
    def tile(x, y, w, dir):
        if w == 0: return
        if check[x][y] == 0:
            if dir != 3:
                floor[x][y] = idx[0]
            if dir != 4:
                floor[x + 1][y] = idx[0]
            if dir != 1:
                floor[x + 1][y + 1] = idx[0]
            if dir != 2:
                floor[x][y + 1] = idx[0]
            check[x][y] = 1
        idx[0] += 1
        w >>= 1
        tile(x, y, w, dir)
        if dir != 3:
            tile(x - w, y - w, w, 1)
        if dir != 4:
            tile(x + w, y - w, w, 2)
        if dir != 1:
            tile(x + w, y + w, w, 3)
        if dir != 2:
            tile(x - w, y + w, w, 4)

    a, b = map(int, input().split())
    a, b = k - b, a - 1
    floor[a][b] = -1
    k >>= 1
    x, y = k - 1, k - 1
    while k:
        dir = 0
        if y < b:
            if x < a:
                dir = 1
            else:
                dir = 2
        else:
            if x >= a:
                dir = 3
            else:
                dir = 4
        tile(x, y, k, dir)
        k >>= 1
        if dir == 1:
            x += k
            y += k
        elif dir == 2:
            x -= k
            y += k
        elif dir == 3:
            x -= k
            y -= k
        else:
            x += k
            y -= k
    for t in floor:
        print(*t)
solution()