https://www.acmicpc.net/problem/32721

| 시간 제한 | 메모리 제한 |
| 1초 | 1024MB |
문제
건덕이가 설립한 오리 왕국은 1부터 N까지 N개의 도시로 이루어져 있다. 각 도시는 다른 도시로 향하는 일방통행 도로를 단 한 개만 가지고 있다. 왕국을 다스리던 건덕이는 어떤 도시에서 도로를 이용해 도달할 수 없는 도시가 있음을 알아챘다.
건덕이는 어떤 도시에서 출발하더라도 모든 도시를 방문할 수 있도록 도로를 최소한으로 수정하기로 했다. 건덕이는 도로를 아래와 같은 방법으로 수정한다.
도시 A에서 출발하는 도로의 목적지를 수정한다. (1 ≤ A ≤ N )
건덕이를 위해 어떤 도시에서 출발하더라도 모든 도시를 방문할 수 있도록 만드는 도로의 최소 수정 횟수를 구해주자!
입력
첫째 줄에 도시의 개수 N이 주어진다. (2 ≤ N ≤ 1,000,000)
둘째 줄에 도시별로 연결된 도시 N개가 공백으로 구분되어 주어진다. i번째 값은 i번째 도시에서 출발하는 도로의 목적지이다. (1 ≤ i ≤ N )
출력
어떤 도시에서 출발하더라도 모든 도시를 방문할 수 있도록 만드는 도로의 최소 수정 횟수를 출력한다.
풀이
다음 상태의 도시들을 살펴봅시다. 문제의 조건에 따르면 9번 도시의 도로는 잘못되었으나, 자기 자신으로 돌아오는 간선을 가진 데이터가 있다고 합니다.

SCC 태그가 달린 문제들을 풀다가 등장했기 때문에 SCC로 접근했습니다. 그런데 모든 정점의 진출차수가 1이라는 제한이 있기 때문인지 정점의 수가 최대 100만개입니다. 깊이 100만의 dfs 재귀를 돌리면 파이썬은 아마 터질거예요.
재귀 호출 없이 스택으로 구현된 코사라주 알고리즘을 사용해볼까 했지만 그래프가 묘하게 단순해보여서 다른 접근 방법을 찾아보기로 했습니다. SCC 아니어도 풀 수 있을 것 같았어요.
먼저 그래프의 구조를 살펴보면 진출차수가 1이기 때문에 진입차수가 0인 정점에서 탐색을 시작한다면 반드시 탐색 경로에 포함된 어떤 지점으로 돌아오는 구간이 있습니다. 즉, 도시들로 만들어진 방향 그래프는 한 가닥으로 이어진 정점들이 크기가 1이상인 사이클로 끝나게 됩니다.
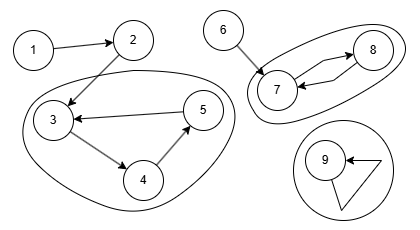
진입차수가 0인 곳에서 시작된 그래프가 사이클이 만들어진 곳에서 무한히 순환하게 됨을 알 수 있습니다. 이 부분을 탐색이 끝나는 지점이라고 생각해봅시다. 사이클의 끝이 탐색했던 곳으로 재진입하는 정점(위 그래프에서는 5, 8, 9)이라고 해보겠습니다.
문제에서 원하는 답은 어떤 정점에서 출발해도 모든 정점을 다 돌아볼 수 있도록 그래프를 수정하는 것입니다. 이런 그래프를 잘 생각해보면 모든 정점의 진출 간선이 그래프의 형태는 딱 한 가지 뿐입니다. 모든 정점이 하나의 사이클을 이루도록 해야 합니다.
아까 그래프를 다시 살펴봤을 때, 사이클의 끝에 해당하는 정점의 진출 간선만 적절히 다른 곳으로 보내주면 모든 정점을 하나의 사이클로 만들 수 있습니다.

5, 8, 9의 간선만 다른 곳으로 보내주면 됩니다. 이때 어디로 보낼 것인지는 중요하지 않습니다. 어쨌든 이 정점들의 진출 간선만 잘 손보면 된다는 거니까요!
이런 지점을 찾으려면 우리는 진입차수가 0인 곳부터 찾아야 합니다. 모든 정점을 다 돌아보면서 진출 간선이 어디를 가리키는지 확인합니다. 한 번도 지목되지 않은 정점은 진입차수가 0이기 때문에 이 정점이 탐색의 출발점이 됩니다.
n = int(input())
a = [0] + list(map(int, input().split()))
indeg = [0] * (n + 1)
for i in range(1, n + 1):
indeg[a[i]] += 1이제 탐색 여부를 관리할 check 배열을 만들고 손봐야 할 부분을 찾아봅니다.
check = [1] * (n + 1)
count = 0
for i in range(1, n + 1):
if indeg[i] == 0:
k = i
while check[k]:
check[k] = 0
k = a[k]
count += 1이제 진입차수가 0인 곳으로부터의 탐색은 끝났습니다. 하지만 아직 남아있는 부분이 있습니다. 아까 그래프의 9번 정점 같은 부분은 스스로가 진입 간선을 만들고 있습니다. 애초에 조건에 맞지 않는 정점이긴 하지만 이 정점이 만약 여러 개의 정점으로 이루어진 하나의 SCC라면 이렇게 됩니다.

1, 2, 3 모든 정점이 진입차수가 있습니다. 이런 식으로 분리된 사이클이 존재하면 진입차수가 0인 부분이 없어서 탐색이 되지 않습니다. 이대로 둔다면 다른 정점에서 이 사이클로 진입할 수 없고, 이 사이클에서도 사이클 밖의 다른 정점에 진입할 수 없습니다. 따라서 이런 사이클도 하나의 정점을 선택해 진출 간선을 다른 곳으로 옮겨줘야 합니다. 하지만 만약 이 사이클 외에 다른 정점이 하나도 없다면? 이대로 두면 됩니다. 그런 경우는 앞서 탐색으로 얻은 count 값이 0이 됩니다. 이번에는 이런 진입점이 없는 사이클을 island로 세어줍니다.
island = 0
for i in range(1, n + 1):
if check[i]:
k = i
while check[k]:
check[k] = 0
k = a[k]
island += 1count와 island를 모두 확인한 결과 count가 0인데 island가 1이라면 어떤 간선도 건드릴 필요가 없습니다. 하지만 그렇지 않은 경우는 모든 탐색과 모든 island의 간선을 하나씩 건드려서 서로를 연결시켜줘야 모든 정점을 하나의 사이클로 연결할 수 있습니다. (count + island)
정답 코드
import sys
input = sys.stdin.readline
n = int(input())
a = [0] + list(map(int, input().split()))
indeg = [0] * (n + 1)
for i in range(1, n + 1):
indeg[a[i]] += 1
check = [1] * (n + 1)
count = 0
for i in range(1, n + 1):
if indeg[i] == 0:
k = i
while check[k]:
check[k] = 0
k = a[k]
count += 1
island = 0
for i in range(1, n + 1):
if check[i]:
k = i
while check[k]:
check[k] = 0
k = a[k]
island += 1
if count == 0 and island == 1: print(0)
else: print(count + island)
