
| 시간 제한 | 메모리 제한 |
| 1초 | 1024MB |
문제
코코는 초콜릿 공장을 운영하고 있다. 이 공장의 기계는 초콜릿을 3 * N 크기(가로 N, 세로 3)의 직사각형 덩어리로 생산한다. 코코는 이 덩어리를 floor(3N/2)개의 1 * 2 또는 2 * 1 크기의 초콜릿으로 나누어 판매하려고 한다. 어째서인지 N이 항상 홀수라서, 코코는 1 * 1 조각을 하나 골라서 잘라 먹고 남은 부분을 나누어 팔기로 했다. N의 값과 코코가 먹은 조각의 위치(R행 C열)가 주어졌을 때, 남은 초콜릿 덩어리를 나누는 방법의 수를 계산해보자.
입력
첫 줄에는 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스마다 N, R, C의 값이 한 줄에 주어진다.
- 1 ≤ T ≤ 1e5
- 1 ≤ N ≤ 1e5, N은 홀수
- 1≤ R ≤ 3, 1 ≤ C ≤ N
출력
각 테스트 케이스의 정답을 각 줄에 출력한다. 단, 정답이 매우 클 수 있으므로 정답을 1e9+7로 나눈 나머지를 출력한다.
풀이
정말 오랜만에 풀어보는 DP문제입니다. 우선 이 문제를 풀기 전에 백준 1793번 타일링, 백준 2133번 타일 채우기 문제를 풀어보면 도움이 많이 됩니다. 저는 이미 이전에 풀어봤던 문제라서 아이디어를 끌어왔습니다.
1. 백준 1793번 타일링
2 * N 크기의 보드를 1 * 2, 2 * 1 타일로 채우는 문제는 타일링의 모듈이 적기 때문에 점화식이 매우 쉽게 구성됩니다. i번째 열까지 구성하는 방법의 수 dp[i] = dp[i - 1] + dp[i - 2]입니다.
간략하게 점화식이 구성되는 이유를 설명해보자면 우선 타일이 한 칸 간격으로 엇갈리도록 놓는 것은 배제됩니다. 이렇게 타일을 놓게 되면 반드시 다음 타일도 엇갈린채 놓이게 되고 정해진 보드의 마지막 1 * 1 칸이 반드시 빈 칸으로 남습니다.
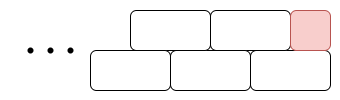
따라서 모든 타일은 세로로 놓거나 가로로 나란히 두 겹을 놓아야 합니다. 그럼 타일을 배치하는 방법은 두 가지 밖에 없습니다.
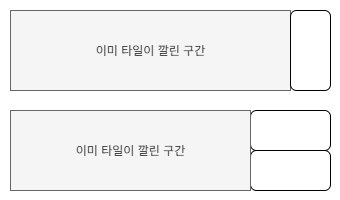
이미 타일이 깔린 구간의 가장 오른쪽에 새로운 타일을 깔아서 2 * i 크기의 보드를 가득 채울 수 있는 방법의 수를 dp[i]라고 해봅시다. 마지막 타일을 깔 수 있는 방법은 위 두 가지 뿐입니다. 이미 타일이 깔린 구간을 구성하는 방법의 수를 이용해 dp[i]의 값을 구성할 수 있습니다. 타일을 세로로 놓는 경우는 dp[i - 1]의 경우를 그대로 가져옵니다. 타일을 가로로 두 겹 놓는 경우는 dp[i - 2]의 경우를 그대로 가져옵니다. 따라서 dp[i] = dp[i - 1] + dp[i - 2]가 됩니다.
2. 백준 2133 타일링
이제 타일을 깔아야 하는 보드의 크기가 3 * N으로 바뀌었습니다. 이제 좀 가짓수가 복잡해집니다. 우선 만약 N이 홀수라면 전체 칸 수도 홀수 개가 됩니다. 타일 자체가 짝수 칸을 채우도록 되어있기 때문에 이 경우는 문제 해결이 불가능합니다. 그래서 2133번 문제에서는 N이 홀수일 때 0을 출력해야 합니다.
타일을 배치할 수 있는 방법을 살펴봅시다.

이런 경우들이 가능한 것 같습니다. 아 그럼 dp[i] = dp[i - 2] * 3으로 하면 되겠네요.

다른 경우가 있습니다. 3행 보드에서는 타일들의 모듈이 무한합니다.

가로 3겹으로 놓인 경우를 제외한다면 모든 짝수 길이의 모듈은 2가지씩 존재합니다. 그리고 여기부터는 무조건 보드의 길이가 짝수이기 때문에 dp[i]를 i * 2번째 열까지 채우는 방법의 수로 정의할게요.
만약 3 * 10의 보드를 채운다고 해봅시다. 이 보드를 가득 채울 수 있는 방법 중에는 먼저 왼쪽에 3 * 4 크기의 보드를 채운 다음, 나머지 3 * 6 크기의 보드를 길이가 6인 모듈로 채우는 방법이 있습니다. 따라서 4 / 6으로 나누어 채우는 방법은 dp[2] * 2가 됩니다.
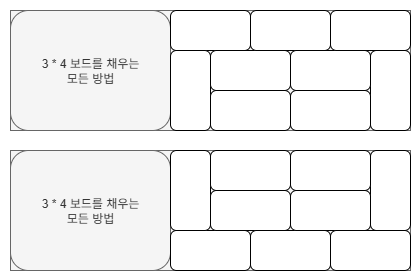
같은 방법으로 왼쪽을 3 * j 크기의 보드를 채우는 모든 방법으로 구성하고 나머지를 2 가지의 모듈로 채울 수 있습니다. 그리고 마지막으로 3 * (i - 1)크기의 보드를 구성하는 방법에 아까 예외로 두었던 가로 3겹의 타일을 까는 1가지 방법만 따로 추가하면 됩니다.
dp[i] = dp[i - 1] * 2 + dp[i - 2] * 2 + ... + dp[1] * 2 + dp[0] * 2 + dp[i - 1] (가로 3겹) = (∑_{j = 0}^{i - 1} dp[j]) * 2 + dp[i - 1]
dp[0]~dp[i - 1]까지의 합은 매 번 구하려면 O(N^2)이기 때문에 누적합으로 처리해 O(N)으로 관리합시다.
3. 백준 25796 초콜릿 나눠 팔기
2133번 문제에 한 가지 조건이 추가되었습니다. 임의의 위치에서 1 * 1크기의 칸이 채워진 상태로 타일링을 하는 문제입니다. 칸 수가 짝수 개여야 하므로 이제 N이 홀수입니다.

만약 2행 1열이 채워진 상태로 타일링을 한다고 해봅시다. 이런 경우 1행과 3행의 1열 칸을 반드시 채워 넣고 시작해야 합니다. 그러면 그 다음엔 2행 2열 칸을 반드시 채워야 합니다. 이 과정이 반복되다가 결국 채우지 못하는 칸이 나타납니다. 이 문제에서는 타일링이 불가능한 케이스가 있습니다.

초기 타일 위치로 주어지면 타일링이 불가능한 곳들입니다. 행과 열 값의 합이 홀수인 곳들입니다. 나머지 경우는 모두 타일링이 가능하겠네요!
그래도 두 가지 케이스가 분리됩니다. 1 * 1 타일이 채워진 위치가 1행인 경우와 3행인 경우는 같다고 볼 수 있습니다. 뒤집으면 똑같은 케이스가 있습니다. 따라서 이 두 가지는 분리하지 않고 같은 것으로 생각합니다. 반면 2행에 채워진 경우는 다른 경우입니다. 이렇게 1 또는 3행에 초기 타일이 있는 경우와 2행에 초기 타일이 있는 경우로 나누어 생각해보겠습니다.
3-1. 1 또는 3행에 초기 타일이 있는 경우

a, b, c 부분으로 타일들의 구역을 나눌 수 있습니다. 1 또는 3행에 초기 타일이 있는 경우는 a와 c의 가로 칸 수가 반드시 짝수이므로 각각 따로 타일링이 가능하고 b도 하나의 타일로 채울 수 있습니다. 이걸 case1이라고 부르겠습니다. case1은 앞서 살펴본 2133 타일링의 점화식으로 해결이 가능합니다. dp[a] * dp[c]입니다.
그런데 b구역을 세로로 놓는 것이 아니라 가로로 놓을 수도 있습니다.
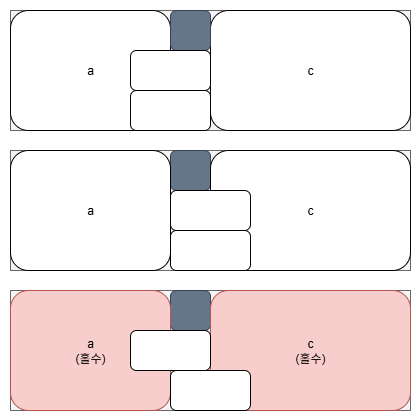
이런 세 가지의 배치가 가능합니다. 세 번쨰 경우는 역시 반대로 놓을 수 있지만 의미는 같습니다. 세 번째 경우는 남는 칸 수가 각각 홀수이기 때문에 채우는 게 불가능합니다. 첫 번째와 두 번째 경우는 좌우를 반대로 놓고 보면 사실 또 같은 경우라고 볼 수 있습니다. 이제 가로의 칸 수가 2x인 직사각형 구역을 채우는 방법의 수를 f(x), 두 번째 경우의 c구역과 같이 가로의 칸 수가 2x인 직사각형에서 한쪽 모퉁이에 1 * 2칸이 덧붙여진 구역을 채우는 방법의 수를 g(x)라고 하겠습니다.

3-2. 2행에 초기 타일이 있는 경우
2행에 초기 타일이 있는 경우는 구역의 모양이 좀 달라져야 할 것 같지만, 잘 보면 초기 타일 주변을 처리하는 경우의 수는 둘 뿐입니다.

초기 타일 위치의 위와 아래를 그림처럼 빨간 타일로 먼저 처리해놓지 않으면 채우는 게 불가능합니다. 한쪽으로 쏠리면 앞서 설명한 이유 때문에 마지막에 2칸이 빈 채로 타일링이 끝납니다. 두 경우 조차 상하 반전 시키면 같은 경우로 볼 수 있습니다. 따라서 우리는 g(n//2 - x) * g(x)를 먼저 구하고 그 두 배만 하면 2행에 초기 타일이 있는 경우의 타일링 방법 수를 알 수 있습니다.
3-3. 전체 경우의 수 구하기
직사각형 구역 f(x) = sigma{y = 0}^{x - 1} (f(y) * 2) * 2 + f(x - 1)
변형 직사각형 구역 g(x) = sigma{y = 0}^{x - 1} (g(y) * 2) + g(x - 1) + 1
정답 코드
code
