
| 시간 제한 | 메모리 제한 |
| 1초 | 128MB |
문제
우리나라 화폐단위, 특히 동전에는 1원, 5원, 10원, 50원, 100원, 500원이 있다. 이 동전들로는 정수의 금액을 만들 수 있으며 그 방법도 여러 가지가 있을 수 있다. 예를 들어, 30원을 만들기 위해서는 1원짜리 30개 또는 10원짜리 2개와 5원짜리 2개 등의 방법이 가능하다.
동전의 종류가 주어질 때에 주어진 금액을 만드는 모든 방법을 세는 프로그램을 작성하시오.
입력
입력의 첫 줄에는 테스트 케이스의 개수 T(1 ≤ T ≤ 10)가 주어진다. 각 테스트 케이스의 첫 번째 줄에는 동전의 가지 수 N(1 ≤ N ≤ 20)이 주어지고 두 번째 줄에는 N가지 동전의 각 금액이 오름차순으로 정렬되어 주어진다. 각 금액은 정수로서 1원부터 10000원까지 있을 수 있으며 공백으로 구분된다. 세 번째 줄에는 주어진 N가지 동전으로 만들어야 할 금액 M(1 ≤ M ≤ 10000)이 주어진다.
편의를 위해 방법의 수는 231 - 1보다 작고, 같은 동전이 여러 번 주어지는 경우는 없다.
출력
각 테스트 케이스에 대해 입력으로 주어지는 N가지 동전으로 금액 M을 만드는 모든 방법의 수를 한 줄에 하나씩 출력한다.
풀이
손쉬운 백트래킹이라 생각해서 바로 짜서 돌려봤지만 제출하기도 전에 첫 예제 1번 테스트 케이스에서 재귀호출을 999번 반복해서 하다가 피토했다. 만약 동전 1원짜리 한 가지로 10000원 만들라고 하면 이 방법은 답이 없긴 하다.
i번째 동전 없이 M원을 만드는 것이 i번째 동전을 사용하고 M원을 만드는 방법의 일부가 될 수 있으므로 dp로 접근할 수 있다.
이 아이디어를 이해하는 게 꽤 어려웠는데 나중에 까먹게 될 나를 위해 설명을 남겨봄...(이걸 보고 다시 이해할 자신은 없지만)

동전들이 2, 3, 8, ...로 주어지는 상황을 가정해보자. k원은 100원으로 설정.
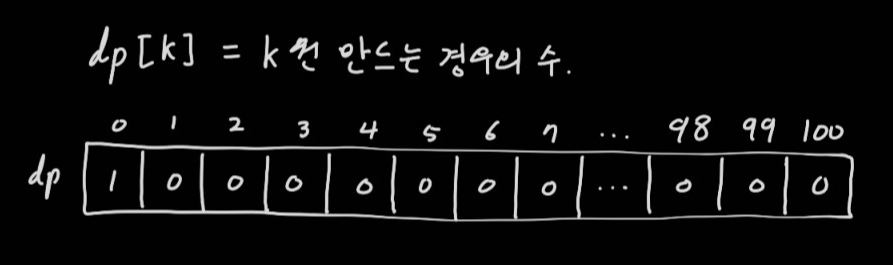
dp[k]는 k원을 만드는 경우의 수를 저장할 배열이다. 이 배열이 2차원이어야 할 것 같은데 의외로 1차원으로 충분하다. 이유는 각 금액별 경우의 수가 연쇄적으로 이전 값을 불러오기 때문이다. dp[0]은 0원을 만드는 경우의 수다. 아무 동전을 사용하지 않는 1가지 경우가 있으므로 1, 나머지는 모두 0으로 초기화한다.
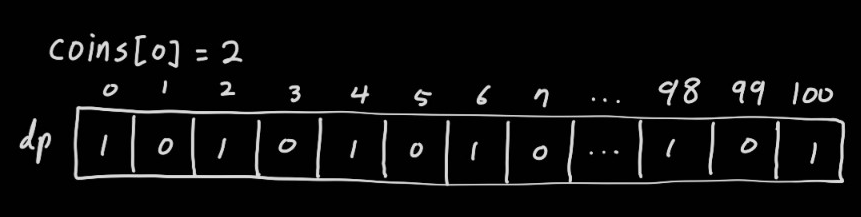
첫번째 동전인 2원으로 경우의 수를 따져본다. 0원을 만드는 경우는 2원을 사용하지 않는 것으로, 이전 값을 그대로 두면 된다. 2원을 만드는 경우는 원래 0이었으나, 0원을 만드는 경우에서 2원 하나를 사용하면 되기 때문에 dp[2] + dp[2 - 2]로 1가지이다. 4원을 만드는 경우는 기존의 4원을 만드는 방법을 그대로 두고, 추가로 2원을 만드는 경우에서 2원을 하나 더 사용하면 된다. dp[4] + dp[4 - 2] = 1. 이런 과정으로 dp[100]까지 채울 수 있다.
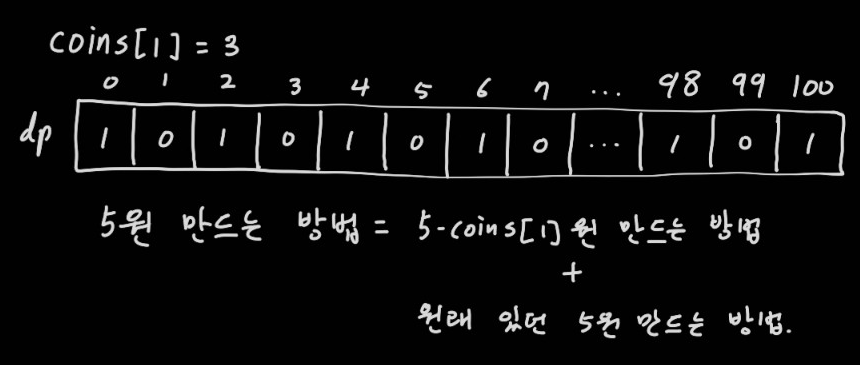
다음 동전 3원으로 3원부터 만들 수 있다. dp[3]에 dp[3 - 3]을 더해주면 되겠다. 이렇게 동전을 순차적으로 사용하여 dp 배열의 값을 건드려주면 경우의 수가 누적 가능하다. 5원을 만드는 방법은 5 - 3원을 만드는 방법과 원래 5원을 만드는 방법을 합한 것과 같다.
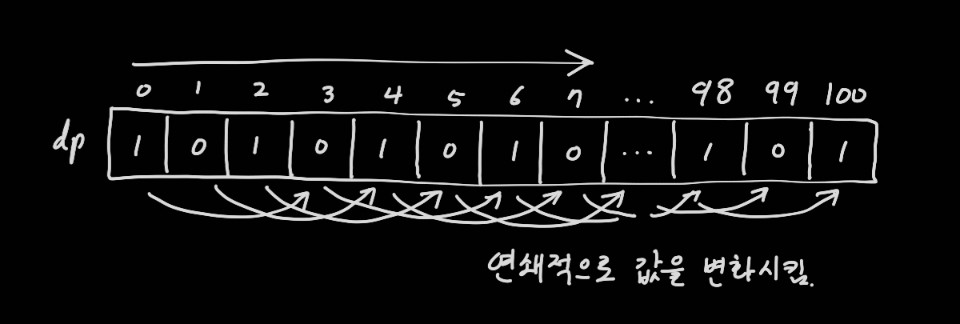
dp[0]이 dp[3]에 영향을 주면 dp[3]은 다시 dp[6]에 영향을 준다. 모든 dp[i]가 dp[i - 동전 액면가]로부터 경우의 수를 끌어올 수 있다.
이렇게 i번째 동전의 액면가를 coins[i], k원을 만드는 방법의 수를 dp[k]라고 하면 dp[k] = dp[k - coin[i]] + dp[k] 라고 할 수 있다.
정답 코드
T = int(input())
for t in range(T):
N = int(input())
coins = list(map(int, input().split()))
M = int(input())
dp = [0 for _ in range(M + 1)]
dp[0] = 1
for i in range(len(coins)):
k = coins[i]
for j in range(1, M + 1):
if k > M:
break
else:
dp[k] += dp[k - coins[i]]
k += 1
print(dp[M])
