10986: 나머지 합

 

시간 제한	메모리 제한
1초	256MB

문제

수 N개 A₁, A₂, ..., A_N이 주어진다. 이때, 연속된 부분 구간의 합이 M으로 나누어 떨어지는 구간의 개수를 구하는 프로그램을 작성하시오.

즉, A_i + ... + A_j (i ≤ j) 의 합이 M으로 나누어 떨어지는 (i, j) 쌍의 개수를 구해야 한다.

 

입력

첫째 줄에 N과 M이 주어진다. (1 ≤ N ≤ 10⁶, 2 ≤ M ≤ 10³)

둘째 줄에 N개의 수 A₁, A₂, ..., A_N이 주어진다. (0 ≤ A_i ≤ 10⁹)

 

출력

첫째 줄에 연속된 부분 구간의 합이 M으로 나누어 떨어지는 구간의 개수를 출력한다.

 

---

풀이

 

1. 1트

누적 합 알고리즘만 써서 제출 해봤더니 시간초과가 떴다.

import sys
input = sys.stdin.readline
N,M = map(int,input().split())
arr = list(map(int,input().split()))
sum = [0]*(N+1)
count = 0
for i in range(1, N+1):
    sum[i] = (sum[i-1]+arr[i-1])

    for j in range(i):
        if (sum[i]-sum[j])%M == 0:
            count += 1
print(count)

그럴 수 밖에 없는 게 테스트 케이스가 매우 많고 나머지를 따로 구해서 합해보는 연산이 매 시도마다 따로 이뤄지기 때문에 시간 복잡도가 O(N²)이다. 테스트 케이스까지 늘어나면 더 오래 걸린다. 나머지를 더 빠르게 연산할 방법을 찾거나 경우의 수를 구할 다른 방법을 찾아야 한다.

 

2. 나머지를 미리 연산해 놓는 방법

O(N)으로 누적 합과 구간 합, 나머지까지 연산할 수 있는 방법을 생각해봤다. 그런데 이 문제는 모든 경우의 수를 찾기 위해 모든 구간 합을 확인해 보아야 하는 이상 O(N²)을 벗어날 수가 없다. 배열 arr의 누적 합 배열 S를 만드는 과정이다.

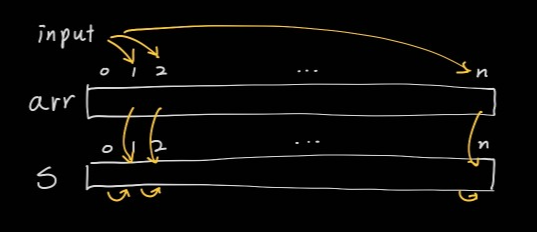
이 과정에서 필요한 연산들을 대강 살펴보면 S[i] = S[i-1]+arr[i]에서 1번의 연산이 필요하다. 총 N개의 수에 대해 같은 연산을 반복하며 수의 크기에 따라 다른 과정이 더 필요하지 않으므로 시간 복잡도는 O(N)이다.

그런데 여기서 구간 합의 나머지가 0이 되는 경우를 모두 찾으려면 모든 구간 합을 탐색해야 한다. 과정은 아래와 같다.

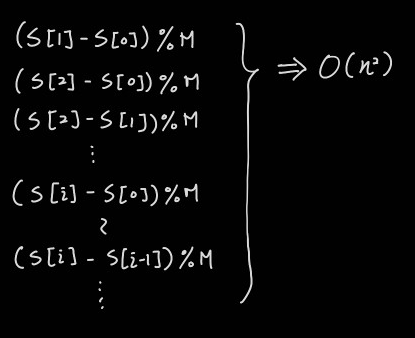
S[1]까지의 구간 합 탐색은 1번, S[2]까지의 탐색은 2번, ... S[i]까지의 탐색은 i번이 이루어지며 S[N-1]까지의 탐색을 끝내면 시간 복잡도는 2차 시간 O(N²)이 된다. N이 100까지 정도의 정수였다면 해볼만 하겠지만 이 문제에서 N는 100만까지이므로 너무 많은 탐색이 필요하다.

 

3. 경우의 수를 빠르게 구하는 방법

구간 합의 나머지가 0이 되는 경우를 살펴보자. (p, q) 구간 합을 M으로 나눈 나머지가 0이라면, (p, q) 구간 합이 S[q]-S[p-1]이므로 이를 M으로 나눈 나머지 역시 0이 된다. 모듈러 연산 법칙에 의해 S[q]와 S[p-1] 각각 M으로 나눈 나머지가 서로 같아야 한다.

그렇다면 어떤 구간 합을 M으로 나눈 나머지가 0이 된다면 그 구간의 시점과 종점의 나머지는 서로 같다. 모든 누적 합에 대해 나머지를 구해놓고 나머지가 같은 두 누적 합 부분을 찾으면 그 구간의 합은 나머지가 0이 된다. 전체 구간합을 두고 나머지가 같은 부분을 2가지씩 뽑는 경우의 수를 구하면 된다.

 

이렇게 나머지가 같은 부분의 시작과 끝을 나타내는 i, j를 하나로 (i, j)쌍이라고 하면 S[i-1], S[j]를 M으로 나눈 나머지는 서로 같으므로 i~j까지의 구간 합은 M으로 나누어 떨어진다.

이렇게 나머지가 같은 부분을 뽑아 구하는 방법으로 (i, j)쌍의 개수를 구할 수 있으니 하나하나 직접 탐색하지 않고 나머지가 같은 누적 합 부분만 찾아주면 된다. S[i]를 M으로 나눈 나머지가 k라면 새로운 M길이의 배열 M의 k 인덱스 값을 1 증가시켜준다.

배열 M의 값을 하나씩 순회하며 M[i]C2를 구하면 된다. 파이썬에서는 math 모듈의 comb를 사용하면 된다.

 

추가로 어떤 풀이에서는 M[i] == 0인 경우는 다른 M[j]와 조합하지 않고 혼자 나머지가 0이므로 따로 세어줘야 한다고 하는데 그렇지 않다. S[0]을 아무 원소도 합하지 않은 것으로 정하고 S[N]까지 탐색한다면 M[i] == 0 인 경우는 (0, i)로 생각할 수 있다. 따라서 아무 원소도 더하지 않아서 누적 합이 0인 상태도 나머지가 0인 것으로 간주하고 M[0]에 추가해주면 같은 효과를 볼 수 있다.

 

정답 코드

import sys
import math
input = sys.stdin.readline
N,M = map(int,input().split())
arr = list(map(int,input().split()))
remain = [0]*M
remain[0] += 1
remain[arr[0]%M] += 1
arr[0] %= M
for i in range(1, N):
    arr[i] = (arr[i-1] + arr[i])%M
    remain[arr[i]] += 1
count = 0
for i in remain:
    if i >= 2:
        count += math.comb(i,2)
print(count)