1. 다익스트라 알고리즘(Dijksrta)
시작 정점으로부터 간선으로 연결된 정점들을 순차적으로 방문한다. 간선의 가중치를 포함해 방문한 정점의 거리가 갱신된다면 방문한 정점에서 이 과정을 다시 반복한다. 원리만 따지면 너비우선탐색과 크게 다르지 않다.
모든 간선의 가중치가 1인 그래프가 주어진다면 너비우선탐색을 실시하는 것이 다익스트라와 같은 효과가 있다.
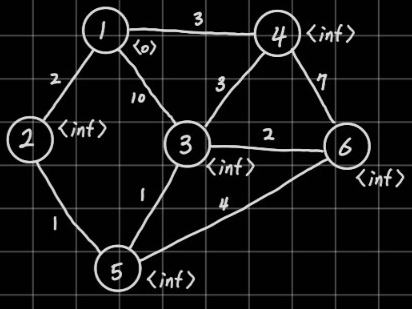
이런 무향 그래프가 있다고 할 때 1에서부터 6까지의 최단거리를 구해보자. 먼저 모든 정점의 거리를 충분히 큰 값인 inf로 설정한다. 실제로 무한일 필요는 없고 탐색하고자 하는 모든 상황에 대해 예상되는 최대 탐색 거리보다 크기만 하면 된다. 최대 정점의 수가 V개이고 간선의 최대 가중치가 W라면 inf는 V*W보다 큰 값이면 된다. 탐색의 출발 정점인 1의 거리는 0이다. 앞으로 방문하는 정점의 거리 값이 현재 탐색에서 얻는 거리보다 짧다면 방문하지 않는다.
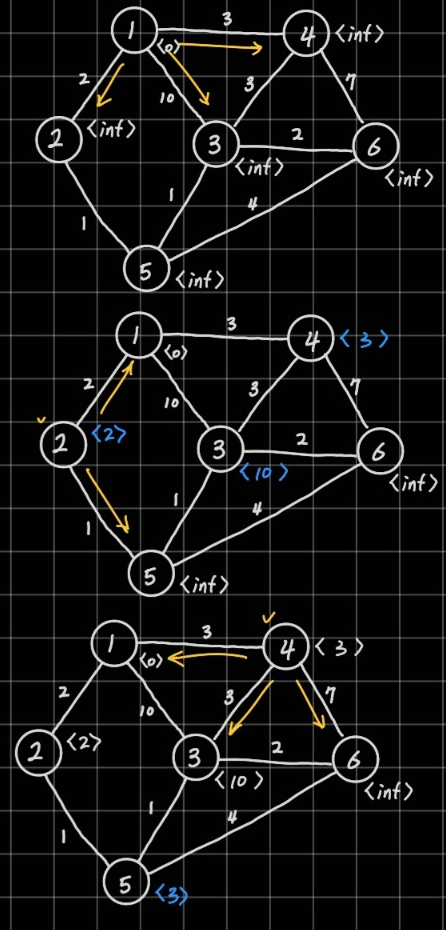
먼저 1에서 2, 3, 4로 이동할 수 있다. 2, 3, 4까지의 현재 거리는 모두 inf이기 때문에 새로 탐색해 얻은 거리로 갱신시켜주고 방문한 노드를 순차적으로 큐에 삽입해 다음에 탐색한다.
2에서 1, 5로 이동할 수 있다. 1로 이동한 경우, 현재 2의 거리에 1로 이어지는 간선의 가중치 2를 더해 4의 거리를 얻었다. 하지만 이미 1까지의 거리는 0으로 저장되었기 때문에 갱신할 수 없다. 5의 경우는 inf가 저장되어있기 때문에 가중치를 더한 3으로 갱신시켜주고 큐에 추가한다.
여기서 일반 큐를 사용하는 경우는 아마 순차적으로 정점을 탐색하기 때문에 3번 정점을 확인할 것이다. 이 경우는 이전에 탐색했던 정점이 갱신될 경우 다시 탐색해야 한다.
다익스트라는 우선순위 큐(priority queue)를 사용해 최적화할 수 있는데 이 경우 저장된 큐에서 현재까지의 거리가 가장 짧은 정점을 먼저 확인한다. 항상 가장 짧은 거리를 먼저 보기 때문에 목적지에 도달한다면 반드시 최단거리임이 보장된다. (단, 모든 간선이 양의 가중치를 갖는다는 조건 하에)
우선순위 큐로 탐색한다면 4번 정점을 확인하게 되며 3번 정점의 거리가 6으로, 6번 정점의 거리가 10으로 갱신된다.
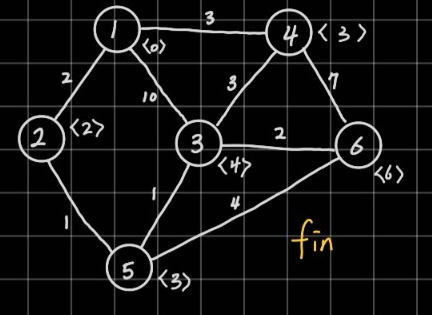
이 과정을 모두 거치면 6까지의 최단 거리는 1-2-5-3-6의 경로로 얻을 수 있는 6이다.
그래프에 음의 가중치를 가진 간선이 있는 경우는 다익스트라 알고리즘으로 최단거리를 찾지 못할 수 있다.
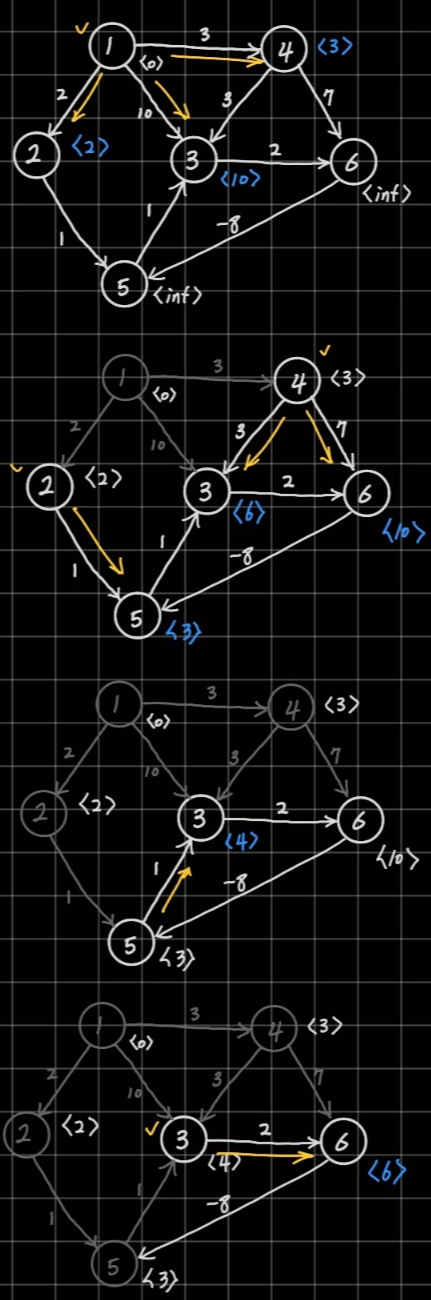
음의 가중치를 가진 간선이 있는 유향 그래프의 탐색을 다익스트라로 수행한다면 결과는 이렇다. 다익스트라는 방문해 이동할 수 있는 모든 간선을 따라 이동을 수행하면 다시 돌아올 필요가 없다.(간선의 가중치가 양수라는 것이 보장되면 원래 그렇다.) 따라서 이번 탐색에서는 간선을 모두 탐색한 정점은 회색으로 칠해 방문할 정점에서 제외한다.
먼저 1에서 2, 3, 4번 정점을 방문하고 각각 갱신시킨다. 1번 정점은 모든 간선을 탐색했으므로 제외된다.
2번 정점에서 5번 정점을 방문해 갱신시키고 4번 정점에서 3번과 6번 정점을 방문해 갱신시킨다. 이때 1번 정점에서 3번 정점을 방문해 큐에 등록된 탐색은 거리 10의 탐색인데 4를 거쳐 3에 온 큐가 거리 6이므로 우선순위를 갖게 된다. 2번, 4번 정점은 모든 간선을 탐색했으므로 제외된다.
5번 정점에서 3번 정점을 방문해 갱신한다. 4번 정점에서 3번 정점을 방문할 때 등록된 큐도 거리가 6이므로 5번을 통해 온 탐색에 우선순위가 밀려나게 된다. 5번 정점은 모든 간선을 탐색했으므로 제외된다.
3번 정점에서 6번 정점을 방문해 갱신시킨다. 3번 정점은 모든 간선을 탐색했으므로 제외된다.
6번 정점을 방문했으므로 탐색은 끝나야 하지만 6번 정점에서 5번 정점을 다시 방문하고 3번 정점을 통해 6번 정점으로 돌아온다면 가중치는 더 줄어들 수 있다. 따라서 이런 경우, 다익스트라 알고리즘 만으로는 최단거리를 얻을 수 없다.(사실 이 경우는 음의 순환고리를 갖는 그래프라서 그런 거다. 예시를 잘 못만들었다. 근데 하여튼 음의 간선이 있으면 최단거리를 찾지 못하는 경우가 있다.)
1-1. 다익스트라 알고리즘 소스코드
다음 소스코드는 i번 정점과 연결된 정점들의 정보가 저장된 graph[i] = [nodes] 형태의 2차원 배열과 출발 정점 start, 목적지 end를 매개변수로 받아 탐색이 가능한 경우, 목적지까지의 최단거리를 반환하고 불가능한 경우 -1을 반환한다.
from heap import heappush, heappop
inf = 1e9
def dijkstra(graph, start, end):
pq = []
V = len(graph)
# 거리 초기화
dist = [inf] * (V+1)
dist[start] = 0
heappush(pq, (0, start))
while pq:
dist_now, node_now = heappop(pq)
# 현재 확인하려는 정점이 탐색할 필요가 없는 경우
if dist[node_now] < dist_now: continue
for node_next, edge_next in graph[node_now]:
dist_new = dist_now + dist_next
# 이전보다 더 짧은 거리인 경우
if dist[node_next] > dist_new:
dist[node_next] = dist_new
heappush(pq, (dist_new, node_next))
if dist[end] == inf: return -1
else: return dist[end]
2. 플로이드-워셜 알고리즘
실생활에서 만나는 문제 상황에서 그래프 내의 간선의 가중치는 거의 항상 양의 정수이지만 특별한 경우, 0 또는 음의 가중치를 갖는 간선이 있기도 하다. 예를 들면 시간여행... 또는 국가간의 환율이 그런 예다.
이 경우, 음의 가중치를 갖더라도 최단거리를 찾을 수 있도록 출발 정점에서 도착 정점을 향한 탐색을 하지 않고 모든 정점에 대해 동시에 탐색을 진행한다. 플로이드-워셜 알고리즘의 핵심 아이디어는 각각의 정점으로부터 모든 정점까지의 연결을 전부 찾아주는 것이다. 말만 들어도 불필요한 탐색이 많아보인다. 당연히 시간복잡도는 다익스트라에 뒤쳐지지만 음의 가중치를 갖는 경우도 탐색 가능하다는 면에서, 또 모든 정점에서 다른 모든 정점까지의 거리를 모두 찾아준다는 점에서 활용도가 높은 알고리즘이다.
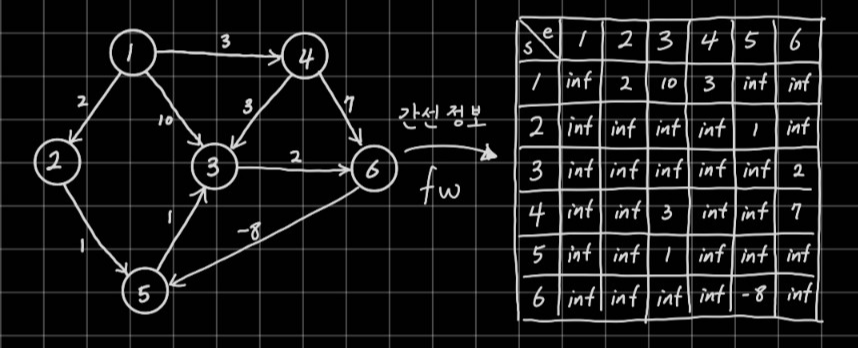
먼저 플로이드-워셜 알고리즘을 수행하기 위해 정점의 수 V에 대해 V*V의 크기를 갖는 2차원 배열을 선언해야 한다. 모든 값을 역시 가능한 최대 거리보다 크게 하고 주어진 간선 정보에 따라 fw[a][b]를 정점 a로부터 정점 b로 이어지는 간선의 가중치로 초기화한다.
탐색은 V개의 모든 정점에 수행하며 각 탐색에서 정점s로부터 정점e로 이동할 때, 정점 m을 거쳐가는 것이 효율적인지를 판단하는 것으로 이루어진다. 점화식을 대강 정리해보면 다음과 같다.
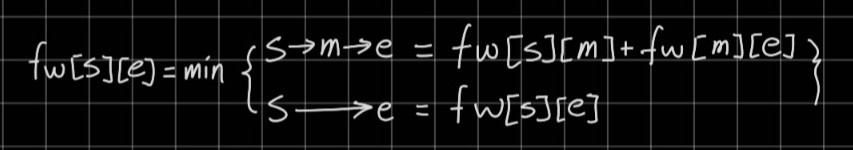
플로이드-워셜 알고리즘은 점화식의 형태를 숙지하고 나면 3중 for문으로 쉽게 구현할 수 있어, 시간 제한이 촉박하지 않다면 그냥 아무렇게나 적용할 수 있는 장점이 있다.(장점 맞나)
2-1. 플로이드-워셜 알고리즘 소스코드
정말 간단하다.
for m in range(1, V+1):
for a in range(1, V+1):
for b in range(1, V+1):
new = fw[a][m] + fw[m][b]
if fw[a][b] > new:
fw[a][b] = new
3. 벨만-포드 알고리즘
플로이드-워셜 알고리즘의 음의 가중치를 갖는 간선이 있어도 적용할 수 있다고 했으나 그런 형태의 모든 그래프에 적용할 수 있는 것은 아니다. 위에서 예시로 제시한 그래프에서도 사실 최단거리를 찾을 수 없다. 그 이유는 이렇다.
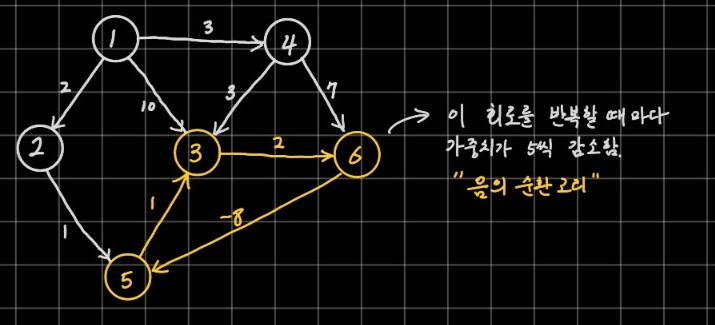
3에서 6에서 5에서 3에서...를 반복하면 1회 반복당 -5의 가중치를 얻는다. 결국 1에서 6까지의 최단거리는 음의 무한대로 뻗어나간다. 이 그래프에 실제로 플로이드-워셜 알고리즘을 적용하면 1부터 6까지의 최단거리는 1로 얻어진다. 이런 경우에는 벨만-포드 알고리즘을 적용해서 음의 순환고리가 포함되었는지를 판단할 수 있다.
벨만-포드 알고리즘은 음의 순환고리가 없는 한, 최단거리를 갖는 경로는 그래프의 모든 정점을 1회 이하로 방문한다는 원리를 이용한다. 전체 정점의 수가 V개 이므로, V-1 회 탐색을 실시하고 V번째 탐색을 실시해 거리의 완화가 발생하면 음의 순환고리가 있는 것이다.
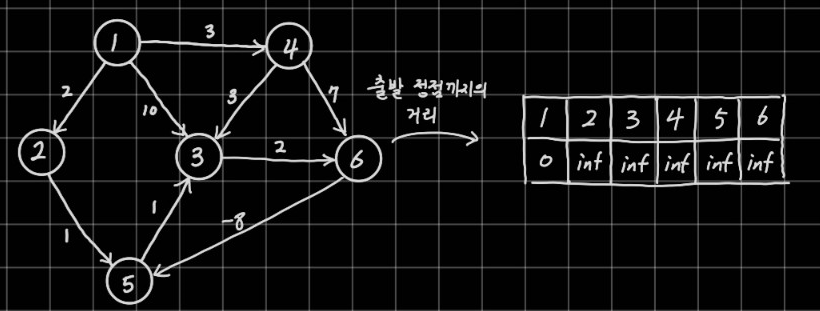
먼저 출발정점으로부터 모든 정점까지의 거리를 inf로 초기화 한다. 역시 최대 거리보다 큰 값을 inf로 설정한다. 1번 정점은 이미 도착해있으므로 초기 값을 0으로 하고 V-1번의 탐색을 실시한다. 매 탐색은 각 정점으로 가중치를 넘겨주며 더 작은 값으로 갱신시켜주는 방식이다.
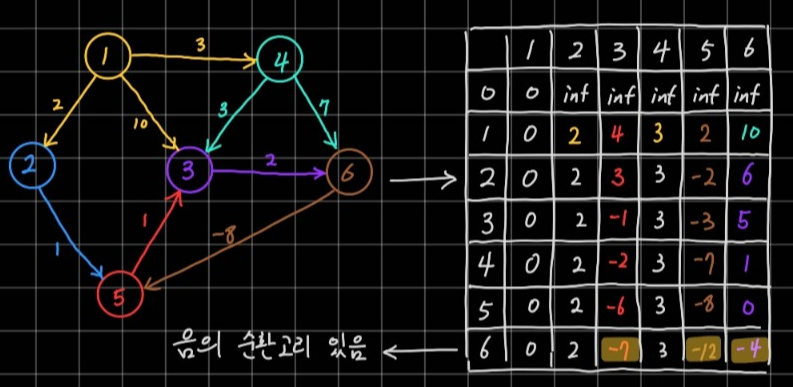
과정을 풀어보면 다음과 같다.
1번째 수행
1번 정점에서 2, 3, 4 갱신
2번 정점에서 5 갱신
3번 정점에서 6 갱신
4번 정점에서 3, 6 갱신
5번 정점에서 3 갱신
6번 정점에서 5 갱신
2번째 수행
1번 정점에서 갱신되는 값 없음
2번 정점에서 갱신되는 값 없음
3번 정점에서 6 갱신
4번 정점에서 갱신되는 값 없음
5번 정점에서 3 갱신
6번 정점에서 5 갱신
...
이 과정을 5번째 수행까지 지속하면, 음의 순환고리가 없는 정점이 6개인 그래프는 반드시 최단거리가 갱신되어있다. 만약 여기서 한 차례 수행을 더 했을 때 거리가 갱신되는 정점이 있다면 음이 순환고리가 있는 그래프다.
