| 시간 제한 | 메모리 제한 |
| 1초 | 512MB |
문제
UCPC에는 N명의 사람이 있다. 먼 옛날 쇼킹핫치킨에 대한 논쟁에서 시작된 이념의 대립으로 UCPC에는 kriii를 따르는 쇼킹핫진보 진영 A와, august14를 따르는 쇼킹핫보수 진영 B의 두 진영이 존재한다. 모든 사람은 둘 중 한 진영에 소속되어 있으며, 두 진영에 동시에 들어가는 것은 불가능하다.
i번 사람과 j번 사람에 대해 서로 다른 진영에 들어가게 될 경우 슬픈 정도 w[i, j]가 주어진다. 일부 사람들은 쇼킹핫에 관한 자신의 철학이 강해 무조건 A진영에 들어가는 사람도 있고, 무조건 B진영에 들어가는 사람도 있다. 물론 치킨은 무엇이든 옳으므로 두 진영 어디에 가든 상관없는 사람도 있다.
N명의 사람들이 적절히 두 진영에 나누어 들어갈 때, 슬픔 정도의 합이 최소가 되게 하라.
입력
첫 번째 줄에는 UCPC 구성원의 수 N(1 ≤ N ≤ 500)이 주어진다. 두 번째 줄에는 N개의 정수가 주어지는데, i번째 수가 1이면 i번 사람은 무조건 A진영에 들어가야 함을, 2라면 무조건 B진영에 들어가야 함을, 0이면 어느 진영에 들어가든지 상관 없다는 것을 의미한다.
세 번째 줄부터 N개의 줄에 걸쳐 i번 사람과 j번 사람이 다른 진영에 들어갈 때의 슬픔 정도 w[i, j]가 주어진다. (i+2)번째 줄에 j번째 수는 w[i, j]를 의미한다. 주어지는 입력은 항상 w[i, j]=w[j, i]를 만족하고, w[i, i]=0이다. w[i, j]는 1,000보다 크지 않은 음이 아닌 정수이다.
출력
첫 줄에 N명의 사람이 A, B 두 진영에 적절히 들어가 슬픈 정도의 합이 최소가 될 때의 슬픔 정도의 합을 출력한다. 두 번째 줄에는 슬픈 정도의 합이 최소가 될 때 A진영에 들어가는 사람들의 번호를 공백으로 구분하여 출력하고, 세 번째 줄에는 슬픈 정도의 합이 최소가 될 때 B진영에 들어가는 사람들의 번호를 공백으로 구분하여 출력한다. 만약 한 진영에 사람이 한 명도 들어가지 않은 경우 빈 줄을 출력한다. 가능한 경우가 여러 가지인 경우 그중 아무거나 하나 출력한다..
풀이
처음 보고 전혀 감이 안왔는데 역시 최대유량이 적용되는 문제다.
1. 최소컷
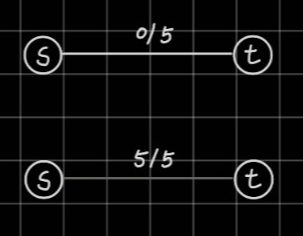
극도로 단순화한 그래프가 있다. 노드는 단 두 개, source와 sink뿐이다. 둘 사이의 유일한 간선이 갖는 용량이 5라면 최대 유량은 5로 마무리된다. 그리고 최대유량 5가 생성되면 source와 sink는 끊어진 것으로 봐도 된다. 이미 생성된 유량은 있지만 현재 상태를 기준으로 변화량을 봤을 때 새로운 유량이 생길 수 없으므로 간선이 없는 것이나 마찬가지다.

이번에는 두 개의 정점이 추가되었다. 이 그래프는 증가경로가 하나 뿐이므로 최대 유량은 잔여유량이 가장 작은 1-2구간의 잔여유량을 따르게 된다. 그리고 여기에서 source와 sink는 역시 끊어진 것으로 볼 수 있다. 그래프가 주어졌을 때, source와 sink를 끊어줄 수 있는 최소한의 유량을 최소컷이라고 한다.
2. 최소컷과 최대유량의 관계

조금 복잡한 그래프를 가져왔다. 무향그래프이고 이 그래프의 최대유량은 18이다. 최대유량을 생성한 후에 잔여유량이 없는 간선을 적절히 선택하면 이렇게 된다.

굵은 회색으로 표시한 간선이 잔여유량이 없는 간선들이다. 이 간선들의 용량을 모두 더하면 최대유량인 18이된다. 그리고 이 간선들을 제거하고 나면 그래프는 빨간색과 파란색으로 분리된다. source와 연결된 쪽, sink와 연결된 쪽이 된다. 최소컷은 최대유량을 생성했을 때 나타나게 된다.
3. 풀이
문제를 보면 A진영 또는 B진영에 확정으로 포함되는 사람들이 있다. 이 사람들은 최소컷으로 절대 분리되어선 안되기 때문에 간선 용량을 매우 큰 값으로 준다. 그리고 나머지 간선은 슬픔의 정도를 그대로 받아서 관리한다.

빨간색 정점은 A진영에 포함되어야 하는 사람, 파란색 정점은 B진영에 포함되어야 하는 사람이고 흰색 정점은 어디로 가든 상관 없는 사람, 흰색 간선은 두 사람이 분리되면 느끼는 슬픔의 정도를 가중치로 갖는다. 가중치는 따로 표시하지 않았지만 여기서 대충 최대유량을 생성시켜보자.

대충 이렇게 되었다고 쳐보자! 회색 간선들은 잔여용량이 더 이상 남지 않은 간선들이다. 이 말은 슬픔의 정도가 이제 더 이상 남지 않았다는 뜻이고 그 슬픔의 양들은 모두 sink로 흘러갔다.

그리고 최대유량이 확인되었다는 것은 더 이상 source에서 sink로 이어지는 증가경로가 존재하지 않는 다는 것이다. 그렇다는 것은 source와 sink가 분리된 것이고 이 것으로 A진영과 B진영으로 나뉠 사람들이 모두 선택되었다. 이 때 끊어진 간선들이 갖는 용량을 모두 더하면 최대유량이고 최소컷과 같다.
와... 이해하는 데 한참 걸렸지만 이해하고 나니까 풀 수 있는 문제가 엄청 많다...
정답 코드
import sys
from collections import deque
input = sys.stdin.readline
inf = int(1e9)
N = int(input())
camp = list(map(int,input().split()))
capa = [[0]*(N+2)]+[[0]+list(map(int, input().split()))+[0] for _ in range(N)]+[[0]*(N+2)]
flow = [[0]*(N+2) for _ in range(N+2)]
work = [0]*(N+2)
level = [-1]*(N+2)
for i in range(N):
if camp[i] == 1: capa[0][i+1] = inf
elif camp[i] == 2: capa[i+1][N+1] = inf
result = 0
while True:
# 레벨 그래프 생성
level = [-1]*(N+2)
level[0] = 0
bfs = deque([0])
while bfs:
now = bfs.popleft()
for next in range(N+2):
if level[next] == -1 and capa[now][next]-flow[now][next] > 0:
level[next] = level[now]+1
bfs.append(next)
if level[-1] == -1: break
# 유량 생성
work = [0]*(N+2)
stack = [(0,inf)]
while stack:
now,cut = stack[-1]
if now == N+1:
for _ in range(level[N+1]):
next,res = stack.pop()
work[stack[-1][0]] -= 1
flow[stack[-1][0]][next] += cut
flow[next][stack[-1][0]] -= cut
result += cut
else:
for next in range(work[now],N+2):
work[now] += 1
residual = capa[now][next]-flow[now][next]
if residual > 0 and level[now]+1 == level[next]:
if cut > residual: cut = residual
stack.append((next,cut))
break
else:
stack.pop()
print(result)
visited = [False]*(N+2)
visited[0] = True
bfs = deque([0])
while bfs:
now = bfs.popleft()
for next in range(1,N+1):
if not(visited[next]) and capa[now][next]-flow[now][next] > 0:
visited[next] = True
bfs.append(next)
A = []
B = []
for i in range(1,N+1):
if visited[i]: A.append(i)
else: B.append(i)
print(*A)
print(*B)