| 시간 제한 | 메모리 제한 |
| 1초 | 512MB |
문제
https://www.acmicpc.net/problem/14750
풀이
다양한 알고리즘이 혼합된 문제다. 하지만 기본 개념 적용만 잘하면 까다로운 부분은 없어서 어렵지 않게 해결 할 수 있는 문제!..(맞나?)
문제에서 요구하는 것은 쥐구멍에 들어갈 수 있는 최대 쥐의 마릿 수다. 쥐는 쥐구멍까지 이어지는 일직선 상에 다른 벽과의 어떤 접점도 없어야만 해당 쥐구멍에 들어갈 수 있고, 각 쥐구멍에는 도망갈 수 있는 쥐의 수 제한이 있다. 우선은 쥐가 어떤 쥐구멍으로 도망갈 수 있는지 확인해야 한다.
1. 선분 교차 판정으로 쥐와 쥐구멍의 연결 여부 확인
쥐의 위치를 m, 쥐구멍의 위치를 h, 벽의 양 끝 점을 a, b라고 하면 아래 그림과 같은 상황에서 ccw 값을 얻을 수 있다. (ccw는 연속한 세 점을 순서대로 이었을 때, 꺾이는 방향이 왼쪽인지 오른쪽인지 확인하게 된다. 왼쪽인 경우 -1을, 오른쪽인 경우 1을, 판단할 수 없는 경우 0을 반환하도록 했다.)
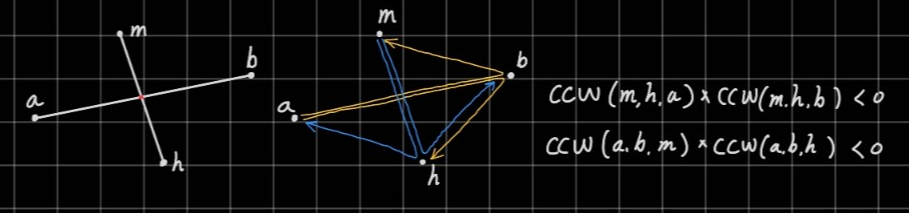
이렇게 한 선분(mh)에 대한 다른 선분(ab)의 양 끝 점으로의 ccw 값을 곱한 결과가 음수라면 선분(ab)의 양 끝 점이 직선(mh)에 대해 다른 곳에 있다는 의미가 되고, 서로의 ccw 곱이 모두 음수라면 두 선분은 반드시 교차하는 것이다. (예외가 존재하지 않는다.) 보통 선분 교차 판정 알고리즘에서는 ccw의 곱이 0인 경우도 포함해서 선분이 끝 점에서 접하는 경우도 교차하는 것으로 본다. 하지만 이 문제에서는 이 경우를 포함해서는 안되는 이유가 있다.

쥐구멍 h는 반드시 벽 위에 존재하므로 벽 ab에 대해 ccw 값이 0이 나오게 된다. 이 때, ccw(a,b,h) = 0의 결과를 교차한 것으로 본다면, 선분 mh에 대해 h가 존재하는 벽 ab의 경우 하나만 교차해야 하므로, mh가 2개 이상의 벽과 교차하면 그 때부터 쥐 m이 쥐구멍 h에 들어갈 수 없는 것으로 봐야 한다. 그리고 선분 ab와 선분 mh가 같은 직선상에 있으면서 겹치는 구간이 있는 경우를 보면 ccw(a,b,h)가 0이고 h가 선분 ab 위에 있지만 쥐구멍 h는 쥐 m에게 사용할 수 없는 쥐구멍이므로 예외처리를 해야 한다.
반대로 이 경우를 교차하지 않는 것으로 본다면 단순히 교차 판정에서만 등호를 빼주는 것으로 끝난다. 이게 더 간단한 것 같아서 이 방법을 선택하기로 했다.
cross 함수를 이렇게 정의 했다. m, h, a, b 점을 매개변수로 받는데 mh가 각각 쥐, 쥐구멍을 잇는 선분, ab가 각각 벽의 양 끝 점을 잇는 선분(벽)이 된다. 이렇게 매개변수로 쥐와 쥐구멍, 벽의 좌표 정보를 구분할 수 있으므로 ccw로 몇 가지 판정을 더 해줄 수 있다. 우선 모든 쥐 m에 대해 for문을 돌리고 그 안에서 모든 쥐구멍 h에 대해 for문을 돌려서 가능한 모든 선분 mh의 경우를 살핀다. 그러면서 주어진 입력의 벽을 순차적으로 모두 확인해 m, h, a, b의 cross를 확인했을 때, 어떤 벽 ab도 쥐의 시선 mh를 가리지 않는다면 쥐 m과 쥐구멍 h는 연결된다.
그리고 쥐의 위치는 벽이 아님이 반드시 보장되므로 ccw(a,b,m) 이 0인 경우는 생각하지 않아도 된다. 있다고 해도 절대 선분 ab 사이에 존재하지 않는다. 그럼 조심해야 하는 것은 두 가지로 좁혀진다. 선분 내에서 교차하는 경우(겹치는 경우 포함), m과 h가 아닌 선분 mh 내의 점에서 벽 ab가 만나는 경우.


먼저 이 경우는 문제가 없다. ccw(a,b,h)는 0이지만 교차가 아니다. 선분 mh에 대한 a와 b의 ccw곱이 음수일 때, ccw(a,b,m)은 절대 0일 수가 없고, ccw(a,b,h)가 만약 0이라면 이건 h가 선분 ab에 위치한 쥐구멍이라는 의미다.
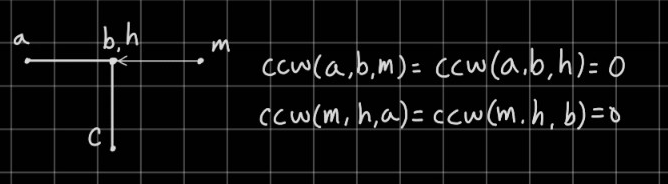
이 경우도 문제가 없다. 모든 ccw가 0인데, h가 a 또는 b와 같은 좌표인 경우다. 이 경우는 나중에 선분의 일부가 겹치는 경우와 분리해줘야 한다. 선분 일부가 겹치는 경우는 쥐구멍이 보이지 않는 것으로 간주해야 한다.
이제 문제가 되는 경우들을 보자.

1)의 경우, 두 선분의 서로에 대한 ccw 곱의 결과는 모두 음수다. 반드시 선분 양 끝이 아닌 내부의 점에서 교차하는 부분이 있고 이 때 h는 m에게 가려진게 되므로 곧바로 쥐 m과 쥐구멍 h를 연결하지 않고 다음 쥐구멍을 확인한다.

2)의 경우, 선분 mh에서 a와 b 중 하나의 ccw만 0인데, 선분 ab에 대해서는 모든 ccw가 0이 아닌 경우다. 이 때는 선분 ab의 한 쪽 끝이 쥐의 시선에 닿은 것이므로 쥐구멍이 가려진다. 곧바로 쥐와 쥐구멍을 연결하지 않고 다음 쥐구멍을 확인한다.

3)의 경우, 선분 mh의 일부와 선분 ab의 일부가 겹친다. 이 때는 모든 ccw가 0이면서 벽의 양 끝 점 중 하나 이상이 mh의 끝을 제외한 내부에 껴있다. 이 경우도 곧바로 쥐와 쥐구멍을 연결하지 않고 다음 쥐구멍을 확인한다.
그래서 순서도로 나타내보면 이런 조건 분기를 거쳐야 한다.

1차적으로 1)의 경우를 판별해 완전히 교차하는지 확인한다.
다음으로 3)의 경우를 먼저 확인해 겹치는 경우를 분리해준다. 이 때 m, h, a, b의 좌표 값을 정렬해 쥐 m과 쥐구멍 h가 배열에서 연속하지 않는다면 반드시 두 선분의 일부가 겹치는 것이므로 쥐와 쥐구멍을 연결하지 않는다.
3)을 만족하지 않는 경우는 선분 mh에 대한 a, b의 ccw를 확인해 둘 중 하나라도 0이라면 선분 ab에 대한 m, h의 ccw 곱이 음수인지 확인한다. 음수라면 a나 b가 선분 mh위에 있는 것이므로 쥐와 쥐구멍을 연결하지 않는다.
2. 연결된 쥐와 쥐구멍 정보로 최대로 숨을 수 있는 쥐의 수 탐색
이제 쥐와 각 쥐에게 보이는 쥐구멍을 선분 교차 판정으로 연결해줬다. 그럼 하나의 그래프가 생성되는데 여기서 풀이가 두 가지로 나뉜다.
먼저 유량 그래프로 보는 방법이다. 모든 쥐들에게 1의 유량으로 연결된 S(source)가 있고 모든 쥐구멍에게 k의 유량으로 연결된 T(sink)가 있다. 쥐와 연결되는 쥐구멍들은 유량 1인 간선으로 이어진다.

S에서 T로 이어지는 증가경로는 쥐가 쥐구멍으로 숨을 수 있는 경로를 의미한다. 따라서 이 유량 그래프의 최대 유량을 구하면 T에 도달한 유량은 각 쥐구멍에 숨은 쥐의 수와 같아진다.
다음은 이분 그래프로 보는 방법이다. 쥐(m)그룹과 쥐구멍(h)그룹으로 나뉜 두 집합을 간선으로 잇는다면 m과 h의 매칭은 쥐 m이 쥐구멍 h로 숨는 것과 같다. 따라서 이런 이분 그래프에서의 최대 매칭은 쥐구멍에 숨을 수 있는 최대 쥐의 마릿 수가 된다.
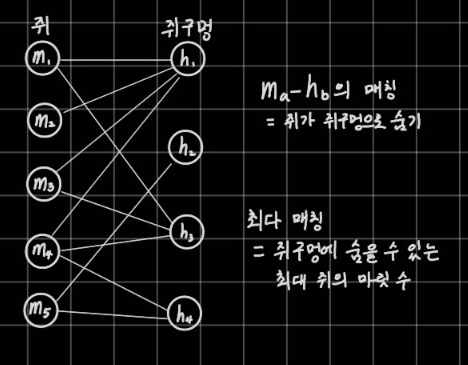
위의 예시는 쥐구멍에 숨을 수 있는 최대 쥐의 수(k)가 1인 경우다. 만약 k가 2라면 각각의 쥐구멍들이 2개로 분리되어 총 h*2개의 정점이 존재해야 하고 문제의 최대 제한인 k = 5인 경우, 쥐구멍의 최대 제한 h = 50일 때 쥐구멍 정점이 250로 처리되어야 한다. 뭔가 많이 복잡해질 것 같지만 정점 번호 관리만 잘 된다면 이분 매칭이 시간 복잡도 면에서 유리하니 더 빠를지도 모르겠다. 정점 분리가 귀찮아서 그냥 디닉 알고리즘을 썼다.
정답 코드
# 14750: Jerry and Tom
import sys
from collections import deque
input = sys.stdin.readline
def connect(u,v,f = 1):
graph[u].append(v)
graph[v].append(u)
capa[u][v] = f
capa[v][u] = 0
flow[u][v] = 0
flow[v][u] = 0
return
def ccw(a,b,c):
k = (a[1]-b[1])*(b[0]-c[0])-(a[0]-b[0])*(b[1]-c[1])
if k > 0: return 1
elif k == 0: return 0
else: return -1
def cross(m, h, a, b):
if h == a or h == b: return True
v1 = ccw(m,h,a)
v2 = ccw(m,h,b)
v3 = ccw(a,b,m)
v4 = ccw(a,b,h)
cross1 = v1*v2
cross2 = v3*v4
# 네 점이 일직선 상에 있을 때
if cross1 == cross2 == 0:
# 쥐구명이 모서리에 있는 경우
l = [m, h, a, b]
if m <= h: l.sort()
else: l.sort(reverse=True)
if not((l[0] == m and l[1] == h) or (l[2] == m and l[3] == h)):
return False
else:
return True
else:
if v4 == 0:
return True
elif cross1 <= 0 and cross2 <= 0:
return False
else:
return True
def lv_graph():
level = [-1]*(m+h+2)
level[0] = 0
bfs = deque([0])
while bfs:
now = bfs.popleft()
for next in graph[now]:
if level[next] == -1 and capa[now][next] - flow[now][next] > 0:
level[next] = level[now]+1
bfs.append(next)
return level
def dinic(now,cut):
if now == m+h+1: return cut
for i in range(work[now],len(graph[now])):
next = graph[now][i]
residual = capa[now][next] - flow[now][next]
if level[now]+1 == level[next] and residual > 0:
f = dinic(next,min(cut,residual))
if f > 0:
flow[now][next] += f
flow[next][now] -= f
return f
work[now] += 1
return 0
n,k,h,m = map(int,input().split())
corner = [tuple(map(int,input().split())) for _ in range(n)]
hole = [tuple(map(int,input().split())) for _ in range(h)]
T = m+h+2
graph = [[] for _ in range(T)]
capa = [{} for _ in range(T)]
flow = [{} for _ in range(T)]
for i in range(1,h+1):
connect(m+i,m+h+1,k)
for i in range(1,m+1):
mouse = tuple(map(int,input().split()))
connect(0,i)
for j in range(h):
insight = True
for w in range(n):
a = corner[w-1]
b = corner[w]
if cross(mouse,hole[j],a,b):
continue
else:
insight = False
break
if insight: connect(i,m+j+1)
hidden = 0
while True:
level = lv_graph()
if level[-1] == -1: break
work = [0]*(m+h+2)
f = dinic(0,int(1e9))
if f == 0: break
else: hidden += f
if hidden == m: print("Possible")
else: print("Impossible")
