[자료구조] 트라이(Trie)

이 Try 아니고

트리 형태의 자료 구조를 말한다.

1. 문자열의 효율적인 탐색 방법

문자열 탐색의 가장 직관적인 방법은 직접 비교해보는 것이다. 한 글자씩 대조해보고 아니면 패스 하는 식. 그러나 이 탐색 방법은 한 가지 하자가 있는데 바로... 일대다 매칭(여러 후보 중에 특정 값과 매칭이 되는 값 찾기)에서는 답 없는 탐색 속도를 갖고 있다는 것.

 

문자열의 집합 S가 있다. 이 안에 어떤 문자열 T가 존재하는지 확인하고 싶다. S가 반 친구들 이름 정도의 규모라면 금방 확인 가능하겠지만 브리태니커 백과사전이라면? 하루 종일 찾아도 못찾을 수 있다. 문자열의 집합 S를 하나로 합쳐버릴 방법이 있다면 어떨까? S 안에 있는 무수한 문자들을 하나하나 대조하는 것이 아니라 하나로 합쳐진 S를 한번 훑어보는 것 만으로 T가 포함되는지 아닌지 확인 가능하다면? 이걸 가능하게 하는 방법이 바로 "패턴 매칭"이다. 그중, 문자열의 맨 앞부분, 접두사(prefix)부터 쭉 확인하는 것을 "트라이(Trie)"라고 한다.

 

2. 트라이의 구현

트라이를 구현하기 위해서는 문자열의 집합 S를 하나의 트리 형태로 바꿔줄 필요가 있다. 맨 위에 올린 사진을 다시 보자.

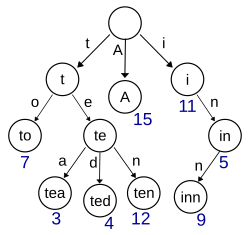
이 트리는 문자열의 집합을 표현한 트라이가 되시겠다. 여기에 "ten"이 포함되는지 확인해보자. 먼저 최상위 노드에서 출발해 첫 글자인 t가 존재하는지 살펴본다. t가 존재하니 넘어가보자. 그 다음 글자인 e도 존재한다. te노드로 넘어가서 마지막 글자인 n이 존재하는지 확인해보자. 존재한다. ten은 종단 문자임이 확인되었다. 그렇다면 문자열의 집합 S에는 ten이 포함된다. 트라이는 이런식으로 특정 문자의 유무를 확인한다. 여기서 각각의 노드마다 구현할 것은 세 가지로 추릴 수 있다.

 

1. 노드가 나타내는 값

2. 현재 노드의 하위 노드

3. 현재 노드가 종단 문자인가?

 

트라이 클래스에서 구현할 함수는 일반적으로 두 가지다.

 

1. 트라이에 새 문자열 추가하기

2. 트라이에 특정 문자가 포함되는지 확인하기

 

먼저 노드를 구현해보자.

class Node(object):
    def __init__(self, key, end = False, data = None):
        self.key = key
        self.is_end = end
        self.data = data
        self.children = dict()

key는 현재 노드가 갖고 있는 문자, end는 현재 노드를 끝으로 하는 문자가 있는지, data는 현재까지 이어진 전체 문자열, children은 하위 노드다.

 

트라이를 구현해보자.

class Trie(object):
	# 초기화
    # 트라이를 선언하면 첫 번째 노드가 head가 된다.
    def __init__(self):
        self.head = Node()

	# 새 문자열 삽입
    def insert(self, strings):
    	# head 노드부터 확인한다.
        current_node = self.head
        # 문자열의 첫 문자부터 각각 확인한다.
        for char in strings:
            # 문자 char가 현재 노드의 하위 노드에 없다면
            # 현재 노드의 하위 노드로 char 노드를 생성한다.
            if current_node.children.get(char) is None:
                current_node.children[char] = Node()
            # 현재 노드를 char로 이동
            current_node = current_node.children[char]
        # 마지막 노드를 종단 문자로 설정
        current_node.is_end = True

	# 문자열 탐색
    def search(self, strings):
    	# head 노드부터 확인한다.
        current_node = self.head
        # 찾고자 하는 문자열의 문자를 각각 확인한다.
        for char in strings:
            # 현재 문자 char가 하위 노드에 없다면
            # 트라이에 찾고자하는 문자열은 없는 것이다.
            if current_node.children.get(char) is None:
                return False
            # 아니면 다음 글자 노드로 이동
            current_node = current_node.children[char]
        # 탐색을 마쳤다면 True를 반환
        return True

살짝 머리가 아파오지만 이게 거의 바뀌지 않고 고정으로 사용되기 때문에 한 번 잘 짜놓고 복붙 돌려쓰면 될 것 같다. 다음에 기회가 되면 심화 개념인 KMP와 아호-코라식을 배워보자.