
1. 강한 연결 요소
강한 연결 요소는 그래프에 존재하는 서브 그래프입니다. 각각의 SCC는 하나의 사이클을 이룹니다. 그러므로 하나의 SCC내의 정점 u와 정점 v를 어떤 방법으로 선택해도 u에서 v로 이동하는 경로가 반드시 존재합니다. 그리고 각각의 SCC는 최대한 크게 구성되어야 합니다. 그러니까 하나의 그래프에 여러 SCC가 있을 때 서로 다른 SCC에 포함되는 두 정점간에는 단방향 경로가 존재할 수 있어도 사이클이 존재하는 경우가 하나도 없어야 합니다.

이 그림의 유향그래프에서 여러 사이클을 찾아볼 수 있습니다. {a, d, b}와 {c, f}등이 있습니다. 하지만 이 중 SCC는 없습니다. {a, d, b} 사이클에서 d - b 사이에 e - f를 추가할 수 있습니다. {a, d, e, f, b} 사이클에서 f에서 e를 거쳐 돌아갈 수 있습니다. 이 그래프에서 a에서 출발해 a로 돌아올 수 있는 가장 큰 사이클은 {a, d, e, f, c, b}입니다.
2-1. 타잔 알고리즘(Tarjan's Algorithm)
타잔 알고리즘은 한 번의 DFS로 그래프를 SCC로 분리합니다. 모든 정점의 모든 간선을 확인하므로 시간복잡도는 O(V+E)입니다. 대략적인 과정을 살펴보면 DFS를 시도하며 방문한 정점들을 스택으로 관리하다가 앞서 방문했던 정점으로 돌아갈 수 없는 정점이 나타나면 스택에 쌓인 정점들을 현재 정점까지 꺼내 하나의 SCC로 묶습니다. 왜 이게 가능한지는 탐색 과정을 직접 살펴보면 알 수 있습니다.
앞서 제시했던 그래프를 약간 수정했습니다. 아래 그래프를 DFS로 순회하며 SCC를 구성해보겠습니다. 탐색은 오름차순으로 진행합니다.

먼저 a가 탐색됩니다. a는 스택에 추가되고 몇 번째로 탐색되었는지 기록해둡니다. 이건 소스코드에서 visit배열로 관리하겠습니다.

d가 탐색되고 스택에 추가됩니다.

b가 탐색되고 스택에 추가됩니다. 다음은 a를 탐색하게 됩니다. 여기서 a는 이미 탐색되었으니 방문은 하지 않습니다. 그런데 a의 방문 번호가 더 짧습니다. a로 돌아가면 사이클이 생성됨을 알 수 있습니다. 일단 다음 탐색을 이어갑니다.

다음으로 e를 탐색하고 스택에 추가합니다. e는 b로 돌아갈 수 있지만 역시 이미 탐색되었으니 방문하지 않습니다. b의 방문 번호가 더 짧으므로 사이클이 생성됨을 알 수 있습니다.역시 탐색을 이어갈 수 있으니 계속 합니다.

f가 탐색되고 스택에 추가됩니다.

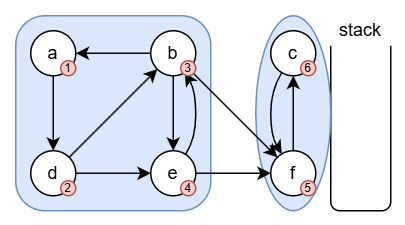
c가 탐색되고 스택에 추가됩니다. 이제 더 이상 탐색할 수 있는 정점이 없습니다. 하지만 c에서 f로 이동하는 간선이 하나 존재하긴 합니다. 타잔 알고리즘에서는 이러한 간선을 무시하지 않고 방문 번호를 확인합니다. c에서 이동할 수 있는 정점 중, 이미 방문을 했으나 아직 SCC로 구성되지 않은 간선에 대해서는 돌아갈 수 있는 가장 작은 정점의 방문 번호를 탐색 결과로 반환합니다. 그러면 DFS를 한층 탈출하며 f를 탐색하는 순서에 c에 대한 탐색 결과로 "5번째 탐색으로 돌아갈 수 있었음"이 반환됩니다.

f에서의 탐색 결과가 자기 자신의 방문 번호와 같습니다. 이 결과가 의미하는 바는, "f에서 이어지는 탐색 트리(그래프이지만 DFS의 결과만 놓고 보면 트리의 형태를 보입니다.)는 f보다 위쪽 정점으로 돌아갈 수 없었음"입니다. f에서는 더 이상 돌아갈 수 있는 정점이 없습니다. 이것을 다시 정리하면 "f에서 시작할 수 있는 탐색의 끝까지 가봤을 때 f로 돌아올 수 있었고, f에서 출발한다면 다시 그 아래에 있는 모든 정점에 도달할 수 있다"는 말이 됩니다. 최대 크기의 사이클이 완성된 것입니다. 스택에 f가 나올 때까지 컴포넌트를 꺼내 SCC를 구성합니다. SCC로 구성된 정점은 소스코드에서 finished 배열로 관리하겠습니다.

e는 b로 돌아갈 수 있습니다. b도 a로 돌아갈 수 있습니다.

a에서는 더 이상 돌아갈 수 있는 정점이 없습니다. 스택에 a가 나올 때까지 컴포넌트를 꺼내 SCC를 구성합니다.
DFS를 끝냈고 스택도 비었습니다. SCC를 모두 찾았습니다.
좀 더 정확한 과정을 나타낸 위키의 설명을 추가합니다.

2-2. 타잔 알고리즘 구현
구현해야 하는 부분들은 다음과 같습니다.
- DFS(돌아갈 수 있는 정점 중 가장 작은 방문 번호를 반환)
- 스택 관리
- 탐색 결과의 방문 번호가 자기 자신인 경우, 스택에서 자신이 나올 때 까지의 컴포넌트를 뽑아 SCC 구성
- 방문한 정점의 방문 번호 관리
- SCC로 구성된 정점 관리
[python3]
from collections import deque
# v, e: 정점, 간선 수
# stack: dfs 스택
# edge: 간선 정보
# back: 되돌아갈 수 있는 정점
# dfs_num: dfs 방문 순서
# visit: 스택 포함 여부
# count: 현재 dfs 방문 순서 관리
# scc: scc 컴포넌트 관리
stack = deque()
back = [i for i in range(v + 1)]
dfs_num = [0] * (v + 1)
visit = [0] * (v + 1)
count = 0
scc = []
def dfs(now):
global count
count += 1
stack.append(now)
visit[now] = 1
back[now] = count
dfs_num[now] = count
for next in edge[now]:
if dfs_num[next] == 0:
dfs(next)
back[now] = min(back[now], back[next])
elif visit[next]:
back[now] = min(back[now], dfs_num[next])
if back[now] == dfs_num[now]:
comp = []
while stack:
comp.append(stack.pop())
visit[comp[-1]] = 0
if now == comp[-1]: break
comp.sort()
scc.append(comp)
for i in range(1, v + 1):
if dfs_num[i] == 0: dfs(i)
scc.sort()
주의할 점은 한 정점에서 시작되는 여러 개의 연결 요소가 탐색되는 경우, 모두 하나의 scc로 연결되어야 합니다.
