| 시간 제한 | 메모리 제한 |
| 2초 | 128MB |
문제
https://www.acmicpc.net/problem/1827
윤화의 직장은 여행을 온 사람들을 버스에서 안내하는 여행 가이드이다. 윤화는 어느 날 다른 날과 다름없이 N명의 사람을 버스 안에서 인솔을 하게 되었다.
그러던 도중 점심시간을 갖게 되었다. 점심시간은 한 시간인데 그 시간동안에는 N명의 사람들은 각자 자기가 가고 싶은 곳으로 갈 수 있다. 한 시간 뒤에 사람들을 버스에서 모이기로 약속을 하고 모두 흩어졌다.
그런데 일이 발생하고 말았다. 한 시간이 흘렀는데 사람들이 아무도 버스에 돌아오지 않은 것이다. 윤화는 흩어진 사람들을 모두 만나서 빨리 버스로 돌아가라고 말을 해 주고 버스로 돌아가야 한다. (단, 그 말을 들은 사람은 그 즉시 자신의 이동 방향을 바꾸어 버스를 향해 이동한다고 가정하여도 좋다.) 그런데 최대한 여행 일정이 늦어지지 않게 하기 위해서 마지막에 버스에 도착하는 사람의 시간을 최소로 하려 한다.
당신이 가지고 있는 정보는 다음과 같다. 점심시간이 끝나는 시각에 N명의 사람들의 위치의 좌표, 그리고 그 사람들의 이동 속도, 그리고 그 사람이 현재 이동하고 있는 방향이 주어진다. (모든 사람은 직선으로만 이동을 한다)
입력
첫째 줄에는 사람의 수 N(1≤N≤8)이 주어진다. 그리고 두 번째 줄에는 당신의 이동 속도가 소수로 주어진다. 그리고 세 번째 줄부터 N+2번째 줄 까지 네 개의 소수 xi,yi,vi,ai가 차례로 주어진다. (xi, y1) (-10^6 <=xi,yi<= 10^6)는 점심시간이 끝났을 때 i번째 사람의 좌표를 의미하고, vi(1≤vi≤100)는 i번째 사람의 이동 속도를 의미한다. 그리고 ai(1≤ai≤2파이) 는 그 사람의 이동 방향을 의미한다.
출력
마지막 사람이 도착하는 시간을 소수점 첫째 자리에서 반올림하여 정수로 출력하시오. 답은 항상 1e6 보다 작거나 같다.
풀이
아. 이딴 문제가 있을 수 있다니 코딩 == 수학이다.
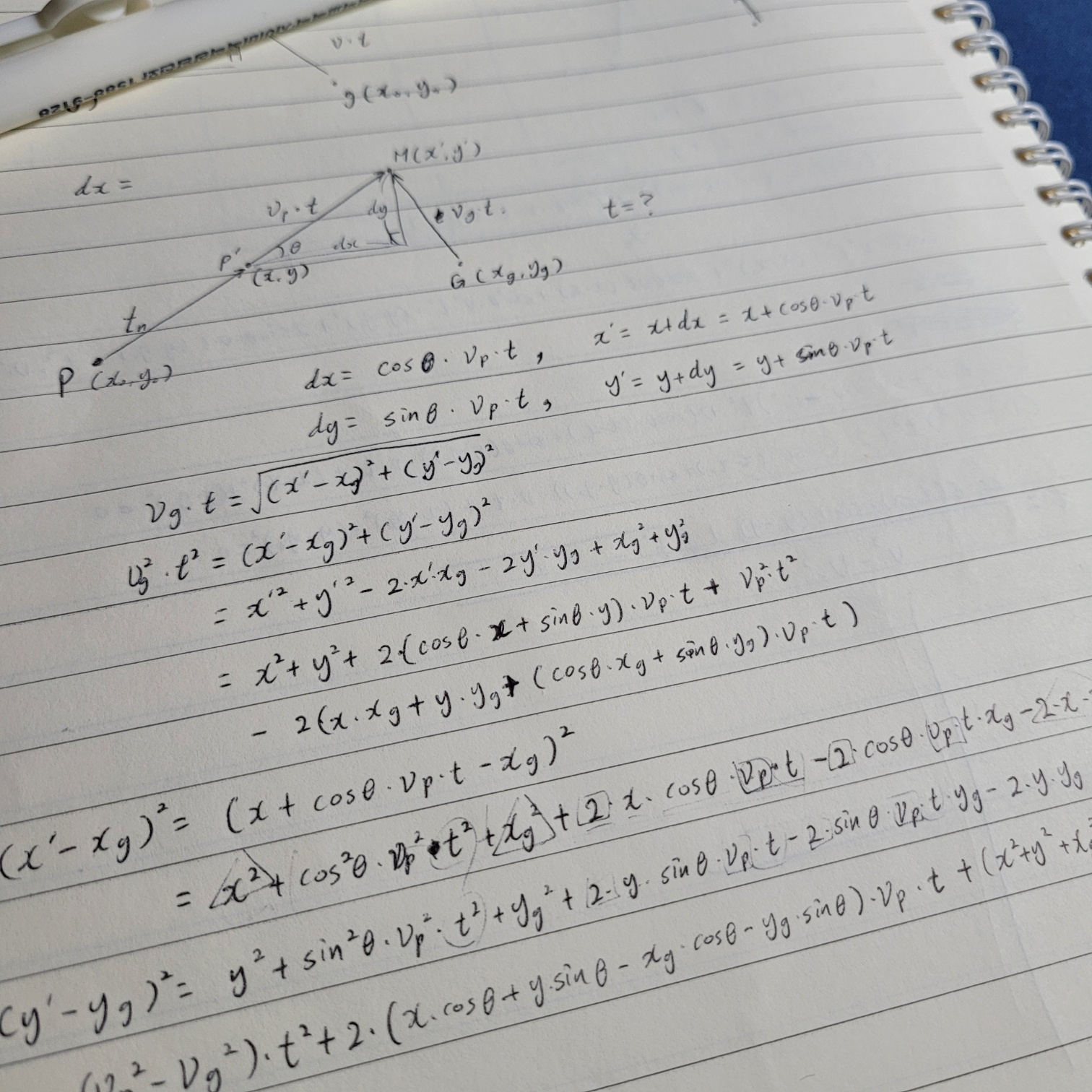
일단 N이 최대 8이므로 가능한 모든 순서를 다 돌아봐도 될 것 같다. 경우의 수로만 따져봐도 1~8번 승객의 방문 순서를 정하는 방법은 8! = 40,320가지이기 때문에 이 정도는 애니악도 우습다. 문제는 '시간을 어떻게 구할 것이냐'인데... 어떤 승객 P가 있고 가이드 G가 있는 상황을 생각해보자.
단순히 G가 P를 향해 직선거리로 이동하게 된다면 G가 초기에 설정한 목적지에 도착했을 때, P는 G가 이동한 시간만큼 이동한 뒤다.
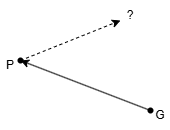
그러면 P의 위치를 계속 업데이트 하며 따라가는 건? 직선거리가 아닌 곡선 경로가 나오게 된다.
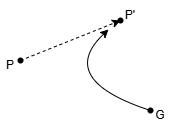
어떤 시간 t가 흘렀을 때 직선으로 운동한 P와 G의 위치가 정확히 같아야 최단시간으로 P를 찾아가게 되는 것이다. 그럼 둘이 만날 수 있는 t를 구해보자.
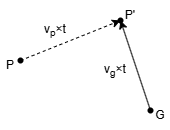
먼저 t시간 동안 P의 좌표가 얼만큼 변할 수 있을까? P의 이동 방향은 호도법으로 주어진다. 각도니까 대충 θ라고 해보자. P가 P'으로 이동한 거리는 P의 속력 vp에 시간 t를 곱한 값과 같으며 P와 P'의 직선거리를 빗변으로 하고 x값의 변화량과 y값의 변화량을 수직으로 만나는 변으로 하는 직각삼각형을 그릴 수 있다.
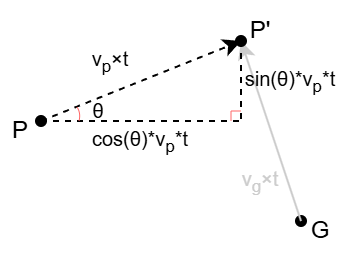
P의 좌표가 (x, y)였다면, P'은 (x + cosθ*vp*t, y + sinθ*vp*t)가 된다. 그리고 가이드 G의 좌표가 (xg, yg)라고 했을 때 P'과 G 사이의 거리를 구할 수 있다.
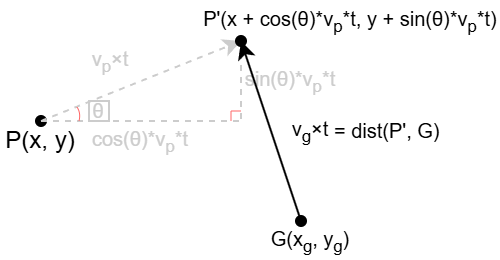
그럼 여기서 vg*t = dist(P', G)로 t에 대한 2차 방정식이 완성된다. 근의 공식을 대입해 2개의 해를 얻을 수 있는데 여기서 두 개의 해는 시간이 바르게 흐르는 경우와 거꾸로 흐르는 경우로, 반드시 두 개의 해 중에서 큰 값을 선택해야 한다.
매 탐색을 시도할 때마다 G의 위치를 이전 P와 만난 P'으로 변경해주고 다음 탐색을 이어가면 된다. 탐색 깊이가 깊어짐에 따라 각각의 P와 P'에서 만났을 때의 시점으로부터 P'과 원점까지의 거리를 P의 속도로 나누어 복귀 시간을 구할 수 있다. 가장 긴 복귀 시간을 최대 깊이에서 확인하고 가장 짧았던 최대 복귀 시간과 비교해 가장 짧은 최대 복귀 시간을 갱신시킨다.
수식 정리도 어렵지만 와... 디버깅이 진짜 토나오는 문제였다. 탐색은 재귀로 구현할 수 있었으나 머리 진짜 터질 것 같아서 그냥 스택으로 구현했다.
정답 코드
import sys
from math import sin, cos
from collections import deque
input = sys.stdin.readline
def get_time(time_n, cor_p, vel_p, dir_p, cor_g, vel_g):
# time_n: 가이드 g가 승객 p를 향해 움직이기 시작한 시각
# cor: 좌표 / vel: 속도 / dir: 방향
x = cor_p[0] + cos(dir_p) * vel_p * time_n
y = cor_p[1] + sin(dir_p) * vel_p * time_n
a = vel_p ** 2 - vel_g ** 2
b = (cos(dir_p) * (x - cor_g[0]) + sin(dir_p) * (y - cor_g[1])) * vel_p
c = (x - cor_g[0]) ** 2 + (y - cor_g[1]) ** 2
time = max(((b ** 2 - a * c) ** 0.5 - b) / a, (-b - (b ** 2 - a * c) ** 0.5) / a)
return time, cor_p[0] + cos(dir_p) * vel_p * (time_n + time), cor_p[1] + sin(dir_p) * vel_p * (time_n + time)
def get_return(time, cor_p, vel_p, dir_p):
x = cos(dir_p) * vel_p * time + cor_p[0]
y = sin(dir_p) * vel_p * time + cor_p[1]
return time + ((x ** 2 + y ** 2) ** 0.5 / vel_p)
def solution():
n = int(input())
velocity = float(input())
people = [list(map(float, input().split())) for _ in range(n)]
result = 1e6
find = deque([(0, 0, 0, 0, 0)])
while find:
mask, time, gx, gy, p_arr = find.pop()
if mask == (1 << n) - 1:
if result > p_arr: result = p_arr
continue
for i in range(n):
if mask & 1 << i: continue
next_time, px, py = get_time(time, (people[i][0], people[i][1]), people[i][2], people[i][3], (gx, gy), velocity)
new_time = next_time + time
arr = get_return(new_time, (people[i][0], people[i][1]), people[i][2], people[i][3])
find.append((mask | 1 << i, new_time, px, py, max(p_arr, arr)))
print(round(result))
solution()
| 시간 제한 | 메모리 제한 |
| 2초 | 128MB |
문제
https://www.acmicpc.net/problem/1827
윤화의 직장은 여행을 온 사람들을 버스에서 안내하는 여행 가이드이다. 윤화는 어느 날 다른 날과 다름없이 N명의 사람을 버스 안에서 인솔을 하게 되었다.
그러던 도중 점심시간을 갖게 되었다. 점심시간은 한 시간인데 그 시간동안에는 N명의 사람들은 각자 자기가 가고 싶은 곳으로 갈 수 있다. 한 시간 뒤에 사람들을 버스에서 모이기로 약속을 하고 모두 흩어졌다.
그런데 일이 발생하고 말았다. 한 시간이 흘렀는데 사람들이 아무도 버스에 돌아오지 않은 것이다. 윤화는 흩어진 사람들을 모두 만나서 빨리 버스로 돌아가라고 말을 해 주고 버스로 돌아가야 한다. (단, 그 말을 들은 사람은 그 즉시 자신의 이동 방향을 바꾸어 버스를 향해 이동한다고 가정하여도 좋다.) 그런데 최대한 여행 일정이 늦어지지 않게 하기 위해서 마지막에 버스에 도착하는 사람의 시간을 최소로 하려 한다.
당신이 가지고 있는 정보는 다음과 같다. 점심시간이 끝나는 시각에 N명의 사람들의 위치의 좌표, 그리고 그 사람들의 이동 속도, 그리고 그 사람이 현재 이동하고 있는 방향이 주어진다. (모든 사람은 직선으로만 이동을 한다)
입력
첫째 줄에는 사람의 수 N(1≤N≤8)이 주어진다. 그리고 두 번째 줄에는 당신의 이동 속도가 소수로 주어진다. 그리고 세 번째 줄부터 N+2번째 줄 까지 네 개의 소수 xi,yi,vi,ai가 차례로 주어진다. (xi, y1) (-10^6 <=xi,yi<= 10^6)는 점심시간이 끝났을 때 i번째 사람의 좌표를 의미하고, vi(1≤vi≤100)는 i번째 사람의 이동 속도를 의미한다. 그리고 ai(1≤ai≤2파이) 는 그 사람의 이동 방향을 의미한다.
출력
마지막 사람이 도착하는 시간을 소수점 첫째 자리에서 반올림하여 정수로 출력하시오. 답은 항상 1e6 보다 작거나 같다.
풀이
아. 이딴 문제가 있을 수 있다니 코딩 == 수학이다.
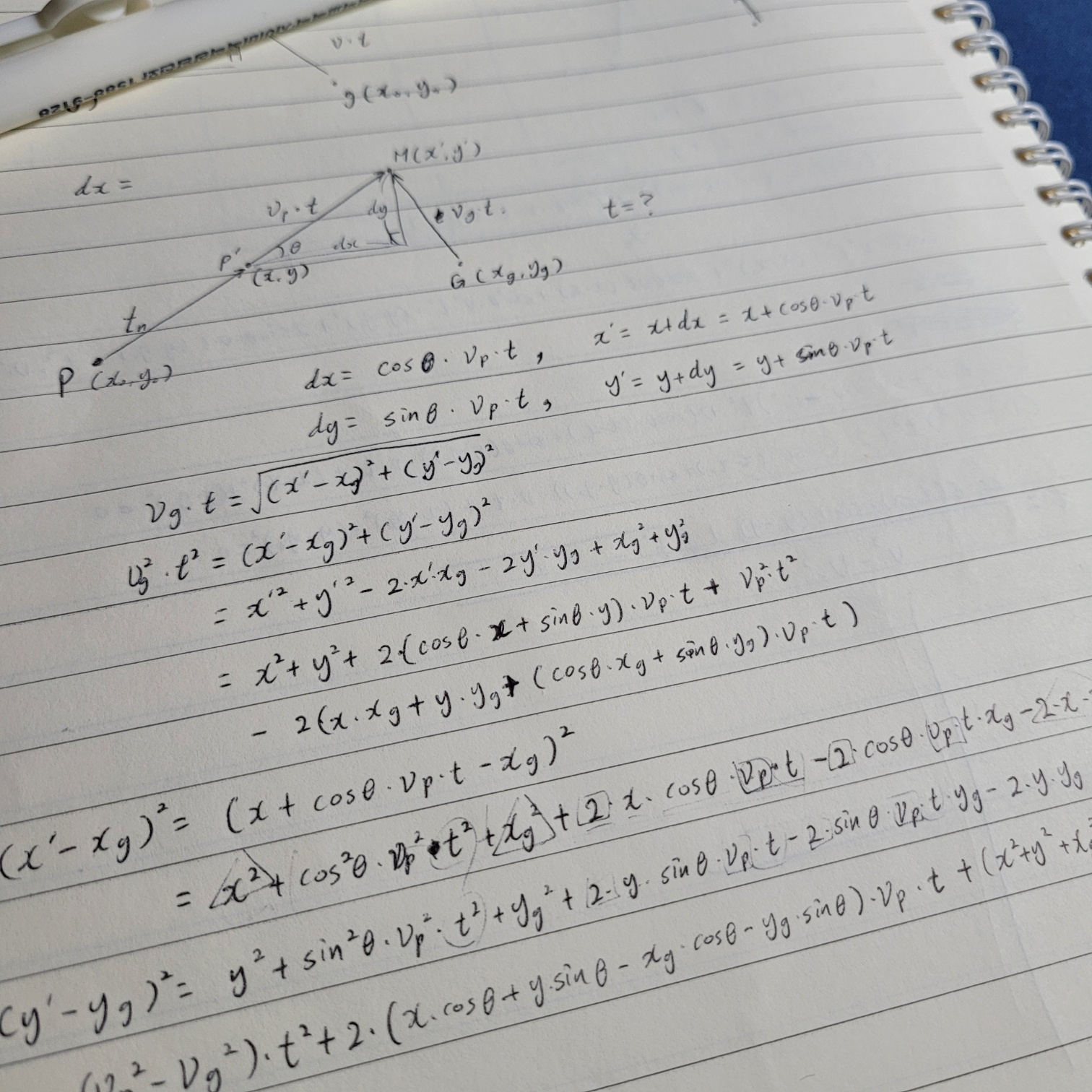
일단 N이 최대 8이므로 가능한 모든 순서를 다 돌아봐도 될 것 같다. 경우의 수로만 따져봐도 1~8번 승객의 방문 순서를 정하는 방법은 8! = 40,320가지이기 때문에 이 정도는 애니악도 우습다. 문제는 '시간을 어떻게 구할 것이냐'인데... 어떤 승객 P가 있고 가이드 G가 있는 상황을 생각해보자.
단순히 G가 P를 향해 직선거리로 이동하게 된다면 G가 초기에 설정한 목적지에 도착했을 때, P는 G가 이동한 시간만큼 이동한 뒤다.

그러면 P의 위치를 계속 업데이트 하며 따라가는 건? 직선거리가 아닌 곡선 경로가 나오게 된다.

어떤 시간 t가 흘렀을 때 직선으로 운동한 P와 G의 위치가 정확히 같아야 최단시간으로 P를 찾아가게 되는 것이다. 그럼 둘이 만날 수 있는 t를 구해보자.

먼저 t시간 동안 P의 좌표가 얼만큼 변할 수 있을까? P의 이동 방향은 호도법으로 주어진다. 각도니까 대충 θ라고 해보자. P가 P'으로 이동한 거리는 P의 속력 vp에 시간 t를 곱한 값과 같으며 P와 P'의 직선거리를 빗변으로 하고 x값의 변화량과 y값의 변화량을 수직으로 만나는 변으로 하는 직각삼각형을 그릴 수 있다.

P의 좌표가 (x, y)였다면, P'은 (x + cosθ*vp*t, y + sinθ*vp*t)가 된다. 그리고 가이드 G의 좌표가 (xg, yg)라고 했을 때 P'과 G 사이의 거리를 구할 수 있다.

그럼 여기서 vg*t = dist(P', G)로 t에 대한 2차 방정식이 완성된다. 근의 공식을 대입해 2개의 해를 얻을 수 있는데 여기서 두 개의 해는 시간이 바르게 흐르는 경우와 거꾸로 흐르는 경우로, 반드시 두 개의 해 중에서 큰 값을 선택해야 한다.
매 탐색을 시도할 때마다 G의 위치를 이전 P와 만난 P'으로 변경해주고 다음 탐색을 이어가면 된다. 탐색 깊이가 깊어짐에 따라 각각의 P와 P'에서 만났을 때의 시점으로부터 P'과 원점까지의 거리를 P의 속도로 나누어 복귀 시간을 구할 수 있다. 가장 긴 복귀 시간을 최대 깊이에서 확인하고 가장 짧았던 최대 복귀 시간과 비교해 가장 짧은 최대 복귀 시간을 갱신시킨다.
수식 정리도 어렵지만 와... 디버깅이 진짜 토나오는 문제였다. 탐색은 재귀로 구현할 수 있었으나 머리 진짜 터질 것 같아서 그냥 스택으로 구현했다.
정답 코드
import sys
from math import sin, cos
from collections import deque
input = sys.stdin.readline
def get_time(time_n, cor_p, vel_p, dir_p, cor_g, vel_g):
# time_n: 가이드 g가 승객 p를 향해 움직이기 시작한 시각
# cor: 좌표 / vel: 속도 / dir: 방향
x = cor_p[0] + cos(dir_p) * vel_p * time_n
y = cor_p[1] + sin(dir_p) * vel_p * time_n
a = vel_p ** 2 - vel_g ** 2
b = (cos(dir_p) * (x - cor_g[0]) + sin(dir_p) * (y - cor_g[1])) * vel_p
c = (x - cor_g[0]) ** 2 + (y - cor_g[1]) ** 2
time = max(((b ** 2 - a * c) ** 0.5 - b) / a, (-b - (b ** 2 - a * c) ** 0.5) / a)
return time, cor_p[0] + cos(dir_p) * vel_p * (time_n + time), cor_p[1] + sin(dir_p) * vel_p * (time_n + time)
def get_return(time, cor_p, vel_p, dir_p):
x = cos(dir_p) * vel_p * time + cor_p[0]
y = sin(dir_p) * vel_p * time + cor_p[1]
return time + ((x ** 2 + y ** 2) ** 0.5 / vel_p)
def solution():
n = int(input())
velocity = float(input())
people = [list(map(float, input().split())) for _ in range(n)]
result = 1e6
find = deque([(0, 0, 0, 0, 0)])
while find:
mask, time, gx, gy, p_arr = find.pop()
if mask == (1 << n) - 1:
if result > p_arr: result = p_arr
continue
for i in range(n):
if mask & 1 << i: continue
next_time, px, py = get_time(time, (people[i][0], people[i][1]), people[i][2], people[i][3], (gx, gy), velocity)
new_time = next_time + time
arr = get_return(new_time, (people[i][0], people[i][1]), people[i][2], people[i][3])
find.append((mask | 1 << i, new_time, px, py, max(p_arr, arr)))
print(round(result))
solution()
