분할 정복으로 행렬의 곱셈하기(슈트라센 알고리즘, Strassen Algorithm)

1. 행렬의 곱셈

행렬의 곱셈은 단순히 곱셈보다 압도적으로 많은 연산을 필요로 한다. 행렬의 규모가 커질수록 그 정도는 더 심화된다. 행렬의 곱셈은 아래와 같은 규칙을 따른다.

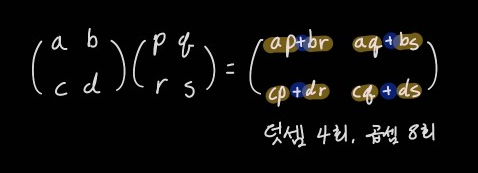
2*2 크기의 정사각행렬 두 개를 곱할 때 필요한 연산은 덧셈 4회, 곱셈 8회이다. 3*3 정사각행렬은 덧셈 18회, 곱셈 27회가 필요하다. 연산 횟수로 보았을 때 n*n크기의 정사각행렬의 곱셈은 O(n³)의 시간복잡도를 갖는다. 지수시간이 아닌게 어디겠냐만 이걸 더 줄이는 알고리즘이 여럿 존재한다. 행렬의 곱셈은 공학분야에서 폭넓게 활용되기 때문에 효율적인 연산 방법을 찾는 연구가 꾸준히 진행되고 있다. 최근에는 구글 딥마인드의 알파제로가 새로운 행렬 곱셈 알고리즘을 발견하기도 했다. 아무튼 다양한 방법 중 깡 삼차시간 연산 방법말고 가장 유명한 "슈트라센(쉬트라센) 알고리즘"을 알아보자.

 

 

2. 전제 조건

슈트라센 알고리즘을 수행하기 위해서는 행렬이 정사각행렬이어야 하며 크기가 2ⁿ*2ⁿ이어야 한다. 그 이유는 분할 정복의 방법을 이용한 알고리즘이기 때문인데 아래와 같이 행렬을 4개의 부분 행렬로 나누어 연산을 수행하기 때문이다.

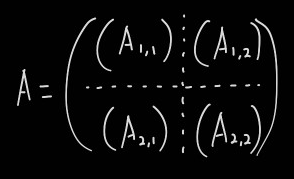
A라는 행렬이 있을 때, 이 행렬은 A_1,1, A_1,2, A_2,1, A_2,2로 나눌 수 있다. 이 때 행렬의 크기가 2의 거듭제곱이어야만 행렬의 분리가 이어질 수 있다. 이 알고리즘에서 행렬의 분리는 최종적으로 1*1 정사각행렬이 될 때까지 이어진다. 그런데 연산할 행렬은 정사각행렬이 아닐수도 있으며 크기도 제각각이다. 이런 경우, 슈트라센 알고리즘은 행렬을 2ⁿ*2ⁿ 정사각행렬로 강제로 늘려버리며 늘어난 칸들은 0으로 채운다. 연산이 끝났을 때 늘렸던 칸을 분리시켜주면 된다.

 

 

3. 부분 행렬의 곱셈

행렬의 곱셈에는 여러가지 법칙이 존재하지만 위에서 설명한 부분 행렬로  곱셈이 가능하다. A와 B 행렬의 곱을 C라고 했을 때, A와 B를 각각 같은 크기의 부분행렬로 나누어 2*2 행렬의 곱셈과 같은 방법으로 연산하면 그 결과는 깡 삼차시간 연산 결과와 같다. 그래서 아래의 부분 행렬로 나눈 곱셈 연산 방법을 정리하면 덧셈이 4회, 곱셈이 8회 필요하다. 이정도면 괜찮은 거 아닌가 싶겠지만 이게 부분 행렬인 것이 함정이다. 만약 A와 B가 128*128 정사각행렬이라면? 덧셈 4회와 곱셈 8회는 더 이상 의미가 없다. (행렬 내부의 연산을 제외하고 덧셈 16,384회, 곱셈 32,768회)

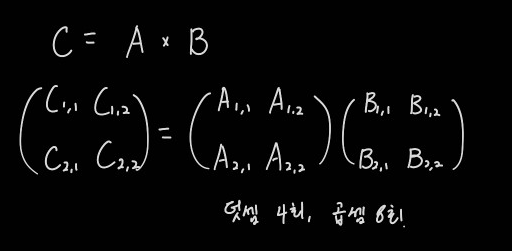
행렬 C의 부분 행렬의 식은 아래와 같다. 편의상 아래첨자는 C11, C12와 같은 식으로 표기한다.

C11 = A11*B11+A12*B21
C12 = A11*B12+A12*B22
C21 = A21*B11+A22*B12
C22 = A21*B12+A22*B22

 

 

4. 슈트라센 알고리즘

슈트라센은 행렬의 곱셈에서 모듈(모듈러 아님) 연산을 수행해 전체 연산 횟수를 줄이는 방법이다. M1~M7까지의 행렬을 새로 정의하면 C의 부분 행렬을 아래와 같이 구할 수 있다. 이 전체 과정에 필요한 연산은 덧셈 18회, 곱셈 7회다. 단순 1회 연산의 수치로 비교하면 기존 깡 삼차시간 연산 방법이 더 효율적이지만 이게 부분 행렬의 연산임을 잊어서는 안된다. 규모가 큰 행렬의 연산에서 곱셈은 덧셈보다 압도적으로 큰 비용이 소요된다. 덧셈 횟수가 4.5배가 되어도 곱셈 횟수를 1회 줄여버린 이 방법이 대규모 행렬의 연산에서는 더 효율적이다.

이 방법을 활용하면 시간복잡도는 O(n^log₂7)이 된다. 하지만 일상적으로 만나는 규모의 행렬에서는 깡 연산이 더 빠르다. 슈트라센 알고리즘이 효율을 발휘하는 건 정말 큰 행렬의 연산이다. chat GPT 형님의 답변에 따르면 32*32 이상의 길이에서나 효율적이라고 한다. 깡 연산으로 쉽게 해결한 백준 2740번 행렬 곱셈 문제에 슈트라센 알고리즘을 적용한 결과 시간초과가 뜬다.

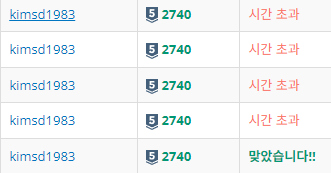
행렬 크기가 64 이상인 경우에만 슈트라센 알고리즘을 적용하도록 했음에도 시간초과였다. 아마 데이터 할당하는 과정과 재귀호출의 반복이 오히려 더 많은 시간을 소모하게 했을 것이다. 이 문제에서는 쓸모 없다...

 

 

5. 소스코드(python)

#행렬의 크기를 2^n*2^n으로 확장
def set_matrix(A,B):
    n = 1
    k = max(len(A),len(A[0]),len(B),len(B[0]))
    while n < k:
        n*=2
    newA = [[0 for _ in range(n)] for __ in range(n)]
    newB = [[0 for _ in range(n)] for __ in range(n)]
    for i in range(len(A)):
        for j in range(len(A[0])):
            newA[i][j] = A[i][j]
    for i in range(len(B)):
        for j in range(len(B[0])):
            newB[i][j] = B[i][j]
    return newA,newB

#행렬의 합
def sum_matrix(A,B):
    n = len(A)
    C = [[0 for _ in range(n)] for __ in range(n)]
    for i in range(n):
        for j in range(n):
            C[i][j] = A[i][j] + B[i][j]
    return C

#행렬의 차
def sub_matrix(A,B):
    n = len(A)
    C = [[0 for _ in range(n)] for __ in range(n)]
    for i in range(n):
        for j in range(n):
            C[i][j] = A[i][j] - B[i][j]
    return C

#행렬을 4개의 부분으로 나누기
def cut_matrix(M):
    n = len(M) // 2
    M11 = [[0 for _ in range(n)] for __ in range(n)]
    M12 = [[0 for _ in range(n)] for __ in range(n)]
    M21 = [[0 for _ in range(n)] for __ in range(n)]
    M22 = [[0 for _ in range(n)] for __ in range(n)]
    for i in range(n):
        for j in range(n):
            M11[i][j] = M[i][j]
            M12[i][j] = M[i][j+n]
            M21[i][j] = M[i+n][j]
            M22[i][j] = M[i+n][j+n]
    return M11,M12,M21,M22

#4개의 부분 행렬을 하나로 합치기
def glue_matrix(C11,C12,C21,C22):
    n = len(C11)
    M = [[0 for _ in range(n*2)] for __ in range(n*2)]
    for i in range(n):
        for j in range(n):
            M[i][j] = C11[i][j]
            M[i][j+n] = C12[i][j]
            M[i+n][j] = C21[i][j]
            M[i+n][j+n] = C22[i][j]
    return M

#행렬의 곱
def mul_matrix(A,B):
    n = len(A)
    if n == 1:
        C = [[0]]
        C[0][0] = A[0][0]*B[0][0]
        return C
    else:
        A11,A12,A21,A22 = cut_matrix(A)
        B11,B12,B21,B22 = cut_matrix(B)
        M1 = mul_matrix(sum_matrix(A11,A22),sum_matrix(B11,B22))
        M2 = mul_matrix(sum_matrix(A21,A22),B11)
        M3 = mul_matrix(A11,sub_matrix(B12,B22))
        M4 = mul_matrix(A22,sub_matrix(B21,B11))
        M5 = mul_matrix(sum_matrix(A11,A12),B22)
        M6 = mul_matrix(sub_matrix(A21,A11),sum_matrix(B11,B12))
        M7 = mul_matrix(sub_matrix(A12,A22),sum_matrix(B21,B22))

        C11 = sum_matrix(sub_matrix(sum_matrix(M1,M4),M5),M7)
        C12 = sum_matrix(M3,M5)
        C21 = sum_matrix(M2,M4)
        C22 = sum_matrix(sum_matrix(sub_matrix(M1,M2),M3),M6)
        return glue_matrix(C11,C12,C21,C22)

#원래 크기로 되돌리기
def trim_matrix(A,row,col):
    M = [[0 for _ in range(col)] for __ in range(row)]
    for i in range(row):
        for j in range(col):
            M[i][j] = A[i][j]
    return M

rowA,colA,rowB,colB = map(int,input().split())
A = [list(map(int,input().split())) for _ in range(rowA)]
B = [list(map(int,input().split())) for _ in range(rowB)]
newA,newB = set_matrix(A,B)
print(trim_matrix(mul_matrix(newA,newB),rowA,colB))

 

 

참고

Python: 행렬 곱셈 알고리즘 소개

이 글에서는 양수만 있는 행렬에 한하여 이차시간의 효율을 갖는 Shrohan Mohapatra의 방법도 소개되어있다.