트리(Tree) 자료구조는 데이터간 위계가 있어 다양한 처리가 가능하다. 세그먼트 트리는 약간의 메모리를 할애해 구간의 값을 따로 관리하여 빠르게 구간 해를 얻도록 하는 트리이다.
세그먼트 트리는 데이터 전체 구간을 반복적으로 이분해 정복하여 구간에서 원하는 값을 저장해 빠르게 얻도록 한다. 원하는 값이라고 한다면 "구간의 합, 곱", "구간 내 최대, 최소 값" 등이 가능하고 분할 정복으로 구간의 해를 얻을 수 있는 문제라면 세그먼트 트리를 적용할 수 있다. 세그먼트 트리는 데이터 접근에서 정확도가 요구되기 때문에 처음에는 구현하기가 매우 까다롭다.(진짜 개고생했다.) 우선 이 글에서는 새로운 데이터를 추가하지 않는 조건에서 세그먼트 트리를 만들고 원하는 구간 해를 출력하는 쿼리를 구현해본다.
1. 트리의 구조
세그먼트 트리는 원본 데이터를 리프노드로, 나머지 노드들은 구간 값을 저장한다. 13개의 데이터를 저장한 세그먼트 트리의 형태는 아래와 같다.
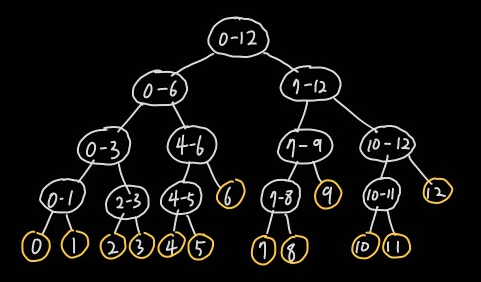
세그먼트 트리는 리프노드(노란색)가 아닌 모든 노드(하얀색)는 자식노드가 항상 둘인 이진트리(Binary Tree)이다. 그리고 원본 데이터는 리프노드에만 저장된다. 트리는 배열로 다룰 수 있다. 배열로 세그먼트 트리를 만들어 관리한다면 각 값의 인덱스는 아래와 같이 부여된다. (인덱스는 0부터 시작하나 편의를 위해 1부터 값을 부여했다.)
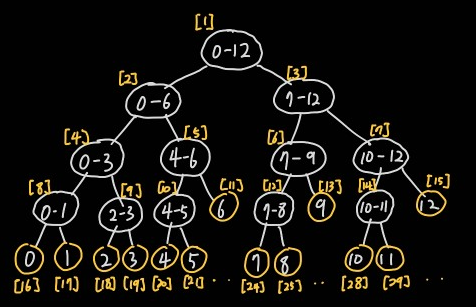
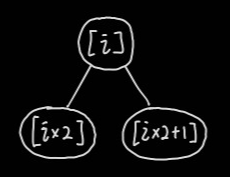
이진트리이므로 부모노드와 자식노드의 인덱스에는 아래와 같은 규칙이 있다. 부모노드는 자식노드의 값을 처리한 결과를 담는다. 이렇게 최상위 노드에는 전체 자료 구간의 해를 담고 하위 계층으로 내려갈수록 나누어진 구간의 값을 저장하게 되는 것이다.
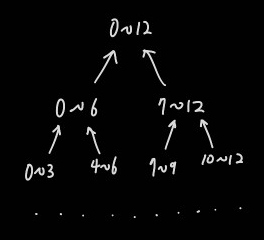
전체 데이터가 2n개 일 때 세그먼트 트리는 완전 이진 트리가 된다. 이 때 가장 깊은 리프노드로부터 최상위 노드까지의 거리를 트리의 높이라고 한다면, 2n개의 데이터를 저장할 세그먼트 트리의 높이는 n이 된다. 여기서 1개의 데이터가 더 있다면 트리의 높이는 n+1이 된다. 따라서 k개의 데이터를 저장할 세그먼트 트리의 높이는 ⌈log2k⌉이고, 세그먼트 트리를 관리할 전체 배열의 길이는 2⌈log2k⌉+1이다.
2-1. 세그먼트 트리 구성 원리
트리의 형태를 잡았으니 이제 데이터를 트리에 담아주고 분할 정복으로 부모노드의 값을 지정해나가면 된다. 임의의 배열 내 구간의 최소값을 저장하는 세그먼트 트리를 만들어보자.
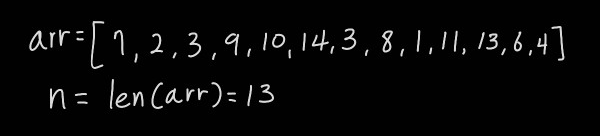
배열은 길이 13인 배열로, 중복인 값도 있고 완전 이진트리가 되지도 않는 어중간한 것으로 만들어봤다. 확실히 만드려면 케이스가 어중간해야 좋더라. 그러면 13개의 데이터의 구간은 어떻게 나누느냐, 양 끝값을 합하고 나눈 것을 왼쪽 구간의 새로운 끝 값으로 설정한다. 그러니까 s가 구간의 시작, e가 구간의 끝이라면 하위 구간 왼쪽 구간의 시작은 s이고 끝은 ⌊(s+e)÷2⌋이다.
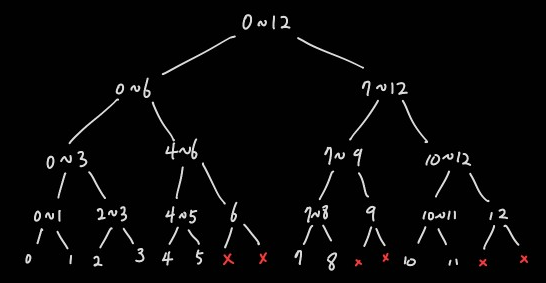
빨간색 x로 표시한 부분은 배열 상으로 존재하는 인덱스이나, 실제로는 사용하지 않는 부분이다. 6, 9, 12의 경우 이 방법으로 구간을 나누었을 때 먼저 완성되는 원소가 하나 뿐인 구간이며 새로운 구간으로 분리가 불가능하다. 따라서 이런 구간이 발생하면 이 노드는 리프노드이며 더 이상 하위 노드를 구성하지 않는다. 각 노드의 값은 아래와 같이 채울 수 있다.


최상위 노드인 0~12 구간의 값을 얻기 위해서는 하위 구간인 0~6 구간과 7~12 구간의 값이 필요하며 그 구간의 값은 다시 하위 구간의 값을 필요로 한다. 따라서 각 노드를 채워 넣는 것은 재귀의 형태를 띠고 있음을 알 수 있다.
2-2. 세그먼트 트리 구성 코드
따라서 세그먼트 트리를 만드는 것은 다음 두 단계로 생각해 볼 수 있다.
- 트리 전체의 크기를 계산한다.
- 양 끝 값의 중간 값으로 하위 구간을 분리해 비교한다.
트리를 저장할 배열의 크기는 앞서 언급했듯이 2⌈log2k⌉+1이다. 따라서 다음과 같이 트리를 선언할 수 있다.(이 트리는 새로운 값을 받지 않는다.)
import math
# 배열을 입력 받는다.
arr = list(map(int,input().split()))
>>> 7 2 3 9 10 14 3 8 1 11 13 6 4
n = len(arr) # 데이터의 개수
h = math.ceil(math.log(n,2)) # 트리의 높이
seg = [0]*(2**(h+1)) # 세그먼트 트리
이제 만들어진 트리 안에 구간의 값을 넣어야 한다. 여기서 트리에 데이터 자체를 넣어도 좋지만, 구간의 최소값은 원본 배열의 인덱스만 있어도 비교가 가능하기 때문에 인덱스를 저장한다. 만약 이 세그먼트 트리가 구간 합, 곱을 저장한다면 인덱스만으로 관리하면 매번 연산을 실시하기 때문에 비효율적이다.
트리에 값을 넣는 함수는 init으로 정의한다. 이 함수는 관리할 트리 전체(tree)와 현재 노드의 트리 내 인덱스(node), 구간의 양 끝 값(s, e)을 매개변수로 받는다. 여기서 주의할 것은 node는 트리의 인덱스이고 구간 양 끝 값인 s, e는 원본 배열 arr의 인덱스라는 점이다. 서로 다른 배열의 인덱스를 동시에 다루다보니 이 부분이 조금 헷갈린다.
"""
arr = [7,2,3,9,10,14,3,8,1,11,13,6,4]
n = len(arr)
h = math.ceil(math.log(n,2))
seg = [0]*(2**(h+1))
"""
def init(tree, node, s, e):
# 양 끝 값이 같아 더 이상 분리할 수 없는 구간인 경우
if s == e:
tree[node] = s
# 양 끝 값이 달라 하위 구간을 나누어 비교해야 하는 경우
else:
m = (s+e)//2 # 구간의 중간
l = node*2 # 왼쪽 구간을 다룰 트리의 인덱스
r = node*2+1 # 오른쪽 구간을 다룰 트리의 인덱스
init(tree, l, s, m) # 하위 구간 중 왼쪽 값 얻기
init(tree, r, m+1, e) # 하위 구간 중 오른쪽 값 얻기
# 하위 구간 값 비교
if arr[tree[l]] <= arr[tree[r]]:
tree[node] = tree[l]
else:
tree[node] = tree[r]
init(seg, 1, 0, n-1)
이렇게 완성된 세그먼트 트리는 아래 그림과 같이 데이터를 저장한다.
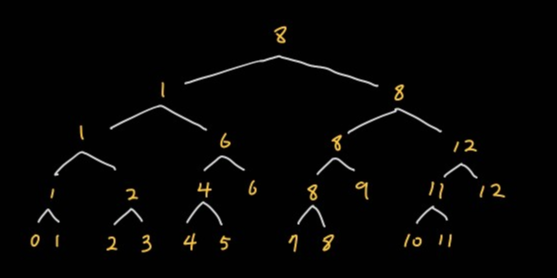
3-1. 쿼리
세그먼트 트리를 완성했다면 원하는 값을 불러올 수 있어야 한다. 구간을 입력했을 때 그 구간의 값이 저장된 트리 노드를 찾아가야 한다. 노드가 가리키는 구간과 원하는 구간의 관계는 아래 세 가지 경우가 있다.
- 원하는 구간이 노드 구간의 양 끝을 모두 포함하는 경우
- 원하는 구간이 노드 구간의 한쪽 끝만 포함하는 경우
- 원하는 구간과 노드 구간이 겹치지 않는 경우
경우의 수만 놓고 보면 여기서 원하는 구간이 노드의 구간에 포함되는 경우도 있지만 탐색 과정에서 이 경우는 따지지 않아도 된다. 그 이유는 다음 각 경우에 따라 탐색을 진행하는 방법을 보면 이해할 수 있다. 찾고자 하는 구간은 3~8이다.
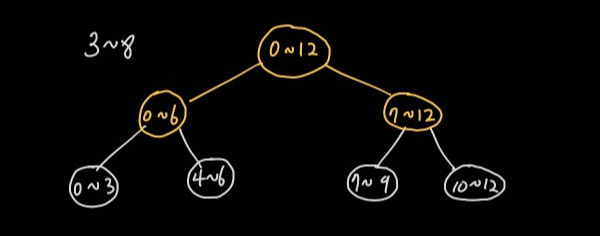
먼저 최상위 노드로 전 구간을 탐색한다. 0~12 구간은 3~8 구간을 완전히 포함한다. 0~12 구간을 좀 더 좁힐 수 있도록 하위 구간을 탐색해야 한다. 탐색이 필요한 노드는 흰색, 탐색한 노드는 노란색, 탐색을 마친 노드는 초록색, 탐색하지 않는 노드는 빨간색으로 표시했다.

0~6 구간은 3~8 구간을 일부 포함한다. 7~12 구간도 마찬가지다. 두 구간 모두 하위 노드를 탐색해야 한다.
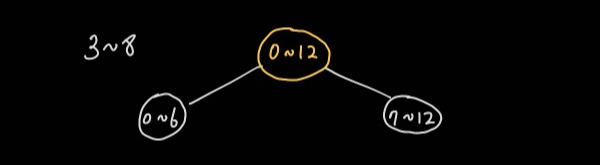
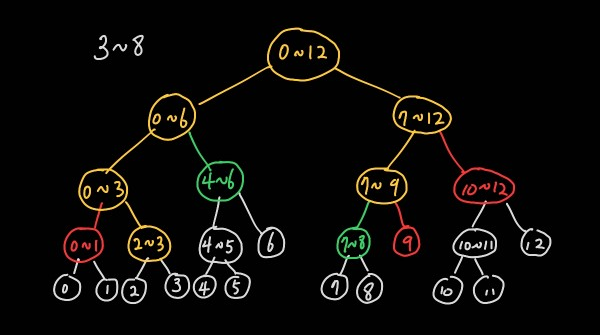
0~3, 7~9 구간은 3~8 구간과 겹치기 때문에 하위 노드 탐색이 필요하다. 4~6 구간은 3~8에 완전히 포함되기 때문에 해당 노드 값만 확인하고 하위 노드 탐색이 필요하지 않다. 10~12 구간은 3~8 구간과 겹치지 않으므로 탐색이 필요하지 않다.
2~3 노드는 하위 노드를 탐색하고 7~8 노드는 하위 노드 탐색이 필요하지 않다. 0~1, 9 노드는 범위 밖이므로 탐색 하지 않는다.

3 노드를 탐색하면 3, 4~6, 7~8 노드를 합해 3~8 구간의 값을 얻을 수 있다.
설명이 깔끔하지 못한 것 같아서 아쉽지만 이게 최선이다... 언젠가 까먹었을 미래의 나는 알아서 잘 해석하도록,,
3-2. 쿼리의 구현
쿼리는 노드가 나타내는 구간과 찾고자 하는 범위의 관계를 따져 경우를 잘 나누어주면 된다. 탐색 과정은 역시 재귀를 통해 구현할 수 있다.
# node = 현재 탐색 중인 노드
# s, e = 노드가 나타내는 구간의 시작과 끝
# l, r = 탐색하려는 구간
def query(tree, node, s, e, l, r):
# 노드의 구간과 탐색 구간이 겹치지 않는 경우
if l > e or r < s:
return -1
# 노드의 구간이 탐색 구간에 완전히 포함되는 경우
if l <= s and e <= r:
return tree[node]
m = (s + e)//2 # 노드 구간 분할 기준
lq = query(tree, node*2, s, m, l, r) # 왼쪽 하위 노드의 값 불러오기
rq = query(tree, node*2+1, m+1, e, l, r) # 오른쪽 하위 노드의 값 불러오기
# 양쪽 하위 노드 쿼리의 결과를 현재 노드 쿼리 결과로 반환하기
if lq == -1 or rq == -1:
return max(lq, rq)
# 하위 노드 쿼리 결과가 -1인 경우, 구간을 벗어난 것이므로 비교하지 않는다.
elif arr[lq] <= arr[rq]:
return lq
else:
return rq
4. 전체 코드
이제 세그먼트 트리와 쿼리를 아래 코드와 같이 구현할 수 있다. 여기서 쿼리로 원하는 구간 양 끝 값을 받을 때, 탐색 가능 여부를 판단해 탐색을 실시한다. 만약 왼쪽 구간 끝이 오른쪽 구간 끝보다 커버리면 무조건 트리의 오른쪽 끝 값을 출력하는 오류가 생긴다. 아무튼 탐색 가능한 범위 안에서만 움직이도록 제한해주면 된다.
import math
# 배열을 입력 받는다.
arr = list(map(int,input().split()))
n = len(arr) # 데이터의 개수
h = math.ceil(math.log(n,2)) # 트리의 높이
seg = [0]*(2**(h+1)) # 세그먼트 트리
#입력된 배열을 최솟값을 저장한 세그먼트 트리로 저장하기
#n = 리프노드의 수
#2^k = n 일 때마다 높이가 k+1인 완전 이진 트리(perfect binary tree)가 된다.
#ceil(log2(n)+1) = 트리의 높이
#2^(ceil(log2(n)+1)) = 필요한 노드의 수
def init(tree, node, s, e):
# 양 끝 값이 같아 더 이상 분리할 수 없는 구간인 경우
if s == e:
tree[node] = s
# 양 끝 값이 달라 하위 구간을 나누어 비교해야 하는 경우
else:
m = (s + e) // 2 # 구간의 중간
l = node * 2 # 왼쪽 구간을 다룰 트리의 인덱스
r = node * 2 + 1 # 오른쪽 구간을 다룰 트리의 인덱스
init(tree, l, s, m) # 하위 구간 중 왼쪽 값 얻기
init(tree, r, m + 1, e) # 하위 구간 중 오른쪽 값 얻기
# 하위 구간 값 비교
if arr[tree[l]] <= arr[tree[r]]:
tree[node] = tree[l]
else:
tree[node] = tree[r]
init(seg, 1, 0, n - 1)
# node = 현재 탐색 중인 노드
# s, e = 노드가 나타내는 구간의 시작과 끝
# l, r = 탐색하려는 구간
def query(tree, node, s, e, l, r):
# 노드의 구간과 탐색 구간이 겹치지 않는 경우
if l > e or r < s:
return -1
# 노드의 구간이 탐색 구간에 완전히 포함되는 경우
if l <= s and e <= r:
return tree[node]
m = (s + e) // 2 # 노드 구간 분할 기준
lq = query(tree, node*2, s, m, l, r) # 왼쪽 하위 노드의 값 불러오기
rq = query(tree, node*2+1, m+1, e, l, r) # 오른쪽 하위 노드의 값 불러오기
# 양쪽 하위 노드 쿼리의 결과를 현재 노드 쿼리 결과로 반환하기
if lq == -1 or rq == -1:
return max(lq, rq)
elif arr[lq] <= arr[rq]:
return lq
else:
return rq
while True:
l, r = map(int,input().split())
if l > r or r < 0 or l > n-1:
print("잘못된 구간 입력")
else:
print(arr[query(seg, 1, 0, n - 1, l, r)])
5. 연습문제
2042: 구간 합 구하기
2042번: 구간 합 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
무난하게 세그먼트 트리를 잘 구현하면 풀 수 있는 문제. 배열 값을 변경한다는 점이 좀 까다로울 수 있지만, 쿼리를 구현해냈다면 노드를 파고들어서 수정하는 것도 가능하다.
11505: 구간 곱 구하기
11505번: 구간 곱 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 곱을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
배열 값이 0인 경우와 탐색하지 않았을 경우 쿼리의 반환 값이 어떻게 되어야 하느냐를 잘 생각해보면 어렵지 않게 풀 수 있다. 다만 파이썬은 노드 값들을 모두 나눠서 저장하지 않으면 시간초과...
트리(Tree) 자료구조는 데이터간 위계가 있어 다양한 처리가 가능하다. 세그먼트 트리는 약간의 메모리를 할애해 구간의 값을 따로 관리하여 빠르게 구간 해를 얻도록 하는 트리이다.
세그먼트 트리는 데이터 전체 구간을 반복적으로 이분해 정복하여 구간에서 원하는 값을 저장해 빠르게 얻도록 한다. 원하는 값이라고 한다면 "구간의 합, 곱", "구간 내 최대, 최소 값" 등이 가능하고 분할 정복으로 구간의 해를 얻을 수 있는 문제라면 세그먼트 트리를 적용할 수 있다. 세그먼트 트리는 데이터 접근에서 정확도가 요구되기 때문에 처음에는 구현하기가 매우 까다롭다.(진짜 개고생했다.) 우선 이 글에서는 새로운 데이터를 추가하지 않는 조건에서 세그먼트 트리를 만들고 원하는 구간 해를 출력하는 쿼리를 구현해본다.
1. 트리의 구조
세그먼트 트리는 원본 데이터를 리프노드로, 나머지 노드들은 구간 값을 저장한다. 13개의 데이터를 저장한 세그먼트 트리의 형태는 아래와 같다.

세그먼트 트리는 리프노드(노란색)가 아닌 모든 노드(하얀색)는 자식노드가 항상 둘인 이진트리(Binary Tree)이다. 그리고 원본 데이터는 리프노드에만 저장된다. 트리는 배열로 다룰 수 있다. 배열로 세그먼트 트리를 만들어 관리한다면 각 값의 인덱스는 아래와 같이 부여된다. (인덱스는 0부터 시작하나 편의를 위해 1부터 값을 부여했다.)


이진트리이므로 부모노드와 자식노드의 인덱스에는 아래와 같은 규칙이 있다. 부모노드는 자식노드의 값을 처리한 결과를 담는다. 이렇게 최상위 노드에는 전체 자료 구간의 해를 담고 하위 계층으로 내려갈수록 나누어진 구간의 값을 저장하게 되는 것이다.

전체 데이터가 2n개 일 때 세그먼트 트리는 완전 이진 트리가 된다. 이 때 가장 깊은 리프노드로부터 최상위 노드까지의 거리를 트리의 높이라고 한다면, 2n개의 데이터를 저장할 세그먼트 트리의 높이는 n이 된다. 여기서 1개의 데이터가 더 있다면 트리의 높이는 n+1이 된다. 따라서 k개의 데이터를 저장할 세그먼트 트리의 높이는 ⌈log2k⌉이고, 세그먼트 트리를 관리할 전체 배열의 길이는 2⌈log2k⌉+1이다.
2-1. 세그먼트 트리 구성 원리
트리의 형태를 잡았으니 이제 데이터를 트리에 담아주고 분할 정복으로 부모노드의 값을 지정해나가면 된다. 임의의 배열 내 구간의 최소값을 저장하는 세그먼트 트리를 만들어보자.
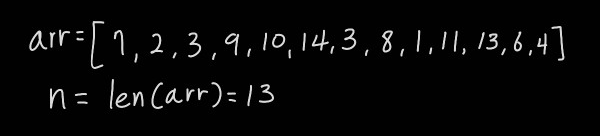
배열은 길이 13인 배열로, 중복인 값도 있고 완전 이진트리가 되지도 않는 어중간한 것으로 만들어봤다. 확실히 만드려면 케이스가 어중간해야 좋더라. 그러면 13개의 데이터의 구간은 어떻게 나누느냐, 양 끝값을 합하고 나눈 것을 왼쪽 구간의 새로운 끝 값으로 설정한다. 그러니까 s가 구간의 시작, e가 구간의 끝이라면 하위 구간 왼쪽 구간의 시작은 s이고 끝은 ⌊(s+e)÷2⌋이다.

빨간색 x로 표시한 부분은 배열 상으로 존재하는 인덱스이나, 실제로는 사용하지 않는 부분이다. 6, 9, 12의 경우 이 방법으로 구간을 나누었을 때 먼저 완성되는 원소가 하나 뿐인 구간이며 새로운 구간으로 분리가 불가능하다. 따라서 이런 구간이 발생하면 이 노드는 리프노드이며 더 이상 하위 노드를 구성하지 않는다. 각 노드의 값은 아래와 같이 채울 수 있다.


최상위 노드인 0~12 구간의 값을 얻기 위해서는 하위 구간인 0~6 구간과 7~12 구간의 값이 필요하며 그 구간의 값은 다시 하위 구간의 값을 필요로 한다. 따라서 각 노드를 채워 넣는 것은 재귀의 형태를 띠고 있음을 알 수 있다.
2-2. 세그먼트 트리 구성 코드
따라서 세그먼트 트리를 만드는 것은 다음 두 단계로 생각해 볼 수 있다.
- 트리 전체의 크기를 계산한다.
- 양 끝 값의 중간 값으로 하위 구간을 분리해 비교한다.
트리를 저장할 배열의 크기는 앞서 언급했듯이 2⌈log2k⌉+1이다. 따라서 다음과 같이 트리를 선언할 수 있다.(이 트리는 새로운 값을 받지 않는다.)
import math
# 배열을 입력 받는다.
arr = list(map(int,input().split()))
>>> 7 2 3 9 10 14 3 8 1 11 13 6 4
n = len(arr) # 데이터의 개수
h = math.ceil(math.log(n,2)) # 트리의 높이
seg = [0]*(2**(h+1)) # 세그먼트 트리
이제 만들어진 트리 안에 구간의 값을 넣어야 한다. 여기서 트리에 데이터 자체를 넣어도 좋지만, 구간의 최소값은 원본 배열의 인덱스만 있어도 비교가 가능하기 때문에 인덱스를 저장한다. 만약 이 세그먼트 트리가 구간 합, 곱을 저장한다면 인덱스만으로 관리하면 매번 연산을 실시하기 때문에 비효율적이다.
트리에 값을 넣는 함수는 init으로 정의한다. 이 함수는 관리할 트리 전체(tree)와 현재 노드의 트리 내 인덱스(node), 구간의 양 끝 값(s, e)을 매개변수로 받는다. 여기서 주의할 것은 node는 트리의 인덱스이고 구간 양 끝 값인 s, e는 원본 배열 arr의 인덱스라는 점이다. 서로 다른 배열의 인덱스를 동시에 다루다보니 이 부분이 조금 헷갈린다.
"""
arr = [7,2,3,9,10,14,3,8,1,11,13,6,4]
n = len(arr)
h = math.ceil(math.log(n,2))
seg = [0]*(2**(h+1))
"""
def init(tree, node, s, e):
# 양 끝 값이 같아 더 이상 분리할 수 없는 구간인 경우
if s == e:
tree[node] = s
# 양 끝 값이 달라 하위 구간을 나누어 비교해야 하는 경우
else:
m = (s+e)//2 # 구간의 중간
l = node*2 # 왼쪽 구간을 다룰 트리의 인덱스
r = node*2+1 # 오른쪽 구간을 다룰 트리의 인덱스
init(tree, l, s, m) # 하위 구간 중 왼쪽 값 얻기
init(tree, r, m+1, e) # 하위 구간 중 오른쪽 값 얻기
# 하위 구간 값 비교
if arr[tree[l]] <= arr[tree[r]]:
tree[node] = tree[l]
else:
tree[node] = tree[r]
init(seg, 1, 0, n-1)
이렇게 완성된 세그먼트 트리는 아래 그림과 같이 데이터를 저장한다.

3-1. 쿼리
세그먼트 트리를 완성했다면 원하는 값을 불러올 수 있어야 한다. 구간을 입력했을 때 그 구간의 값이 저장된 트리 노드를 찾아가야 한다. 노드가 가리키는 구간과 원하는 구간의 관계는 아래 세 가지 경우가 있다.
- 원하는 구간이 노드 구간의 양 끝을 모두 포함하는 경우
- 원하는 구간이 노드 구간의 한쪽 끝만 포함하는 경우
- 원하는 구간과 노드 구간이 겹치지 않는 경우
경우의 수만 놓고 보면 여기서 원하는 구간이 노드의 구간에 포함되는 경우도 있지만 탐색 과정에서 이 경우는 따지지 않아도 된다. 그 이유는 다음 각 경우에 따라 탐색을 진행하는 방법을 보면 이해할 수 있다. 찾고자 하는 구간은 3~8이다.
먼저 최상위 노드로 전 구간을 탐색한다. 0~12 구간은 3~8 구간을 완전히 포함한다. 0~12 구간을 좀 더 좁힐 수 있도록 하위 구간을 탐색해야 한다. 탐색이 필요한 노드는 흰색, 탐색한 노드는 노란색, 탐색을 마친 노드는 초록색, 탐색하지 않는 노드는 빨간색으로 표시했다.

0~6 구간은 3~8 구간을 일부 포함한다. 7~12 구간도 마찬가지다. 두 구간 모두 하위 노드를 탐색해야 한다.

0~3, 7~9 구간은 3~8 구간과 겹치기 때문에 하위 노드 탐색이 필요하다. 4~6 구간은 3~8에 완전히 포함되기 때문에 해당 노드 값만 확인하고 하위 노드 탐색이 필요하지 않다. 10~12 구간은 3~8 구간과 겹치지 않으므로 탐색이 필요하지 않다.

2~3 노드는 하위 노드를 탐색하고 7~8 노드는 하위 노드 탐색이 필요하지 않다. 0~1, 9 노드는 범위 밖이므로 탐색 하지 않는다.

3 노드를 탐색하면 3, 4~6, 7~8 노드를 합해 3~8 구간의 값을 얻을 수 있다.

설명이 깔끔하지 못한 것 같아서 아쉽지만 이게 최선이다... 언젠가 까먹었을 미래의 나는 알아서 잘 해석하도록,,
3-2. 쿼리의 구현
쿼리는 노드가 나타내는 구간과 찾고자 하는 범위의 관계를 따져 경우를 잘 나누어주면 된다. 탐색 과정은 역시 재귀를 통해 구현할 수 있다.
# node = 현재 탐색 중인 노드
# s, e = 노드가 나타내는 구간의 시작과 끝
# l, r = 탐색하려는 구간
def query(tree, node, s, e, l, r):
# 노드의 구간과 탐색 구간이 겹치지 않는 경우
if l > e or r < s:
return -1
# 노드의 구간이 탐색 구간에 완전히 포함되는 경우
if l <= s and e <= r:
return tree[node]
m = (s + e)//2 # 노드 구간 분할 기준
lq = query(tree, node*2, s, m, l, r) # 왼쪽 하위 노드의 값 불러오기
rq = query(tree, node*2+1, m+1, e, l, r) # 오른쪽 하위 노드의 값 불러오기
# 양쪽 하위 노드 쿼리의 결과를 현재 노드 쿼리 결과로 반환하기
if lq == -1 or rq == -1:
return max(lq, rq)
# 하위 노드 쿼리 결과가 -1인 경우, 구간을 벗어난 것이므로 비교하지 않는다.
elif arr[lq] <= arr[rq]:
return lq
else:
return rq
4. 전체 코드
이제 세그먼트 트리와 쿼리를 아래 코드와 같이 구현할 수 있다. 여기서 쿼리로 원하는 구간 양 끝 값을 받을 때, 탐색 가능 여부를 판단해 탐색을 실시한다. 만약 왼쪽 구간 끝이 오른쪽 구간 끝보다 커버리면 무조건 트리의 오른쪽 끝 값을 출력하는 오류가 생긴다. 아무튼 탐색 가능한 범위 안에서만 움직이도록 제한해주면 된다.
import math
# 배열을 입력 받는다.
arr = list(map(int,input().split()))
n = len(arr) # 데이터의 개수
h = math.ceil(math.log(n,2)) # 트리의 높이
seg = [0]*(2**(h+1)) # 세그먼트 트리
#입력된 배열을 최솟값을 저장한 세그먼트 트리로 저장하기
#n = 리프노드의 수
#2^k = n 일 때마다 높이가 k+1인 완전 이진 트리(perfect binary tree)가 된다.
#ceil(log2(n)+1) = 트리의 높이
#2^(ceil(log2(n)+1)) = 필요한 노드의 수
def init(tree, node, s, e):
# 양 끝 값이 같아 더 이상 분리할 수 없는 구간인 경우
if s == e:
tree[node] = s
# 양 끝 값이 달라 하위 구간을 나누어 비교해야 하는 경우
else:
m = (s + e) // 2 # 구간의 중간
l = node * 2 # 왼쪽 구간을 다룰 트리의 인덱스
r = node * 2 + 1 # 오른쪽 구간을 다룰 트리의 인덱스
init(tree, l, s, m) # 하위 구간 중 왼쪽 값 얻기
init(tree, r, m + 1, e) # 하위 구간 중 오른쪽 값 얻기
# 하위 구간 값 비교
if arr[tree[l]] <= arr[tree[r]]:
tree[node] = tree[l]
else:
tree[node] = tree[r]
init(seg, 1, 0, n - 1)
# node = 현재 탐색 중인 노드
# s, e = 노드가 나타내는 구간의 시작과 끝
# l, r = 탐색하려는 구간
def query(tree, node, s, e, l, r):
# 노드의 구간과 탐색 구간이 겹치지 않는 경우
if l > e or r < s:
return -1
# 노드의 구간이 탐색 구간에 완전히 포함되는 경우
if l <= s and e <= r:
return tree[node]
m = (s + e) // 2 # 노드 구간 분할 기준
lq = query(tree, node*2, s, m, l, r) # 왼쪽 하위 노드의 값 불러오기
rq = query(tree, node*2+1, m+1, e, l, r) # 오른쪽 하위 노드의 값 불러오기
# 양쪽 하위 노드 쿼리의 결과를 현재 노드 쿼리 결과로 반환하기
if lq == -1 or rq == -1:
return max(lq, rq)
elif arr[lq] <= arr[rq]:
return lq
else:
return rq
while True:
l, r = map(int,input().split())
if l > r or r < 0 or l > n-1:
print("잘못된 구간 입력")
else:
print(arr[query(seg, 1, 0, n - 1, l, r)])
5. 연습문제
2042: 구간 합 구하기
2042번: 구간 합 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
무난하게 세그먼트 트리를 잘 구현하면 풀 수 있는 문제. 배열 값을 변경한다는 점이 좀 까다로울 수 있지만, 쿼리를 구현해냈다면 노드를 파고들어서 수정하는 것도 가능하다.
11505: 구간 곱 구하기
11505번: 구간 곱 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 곱을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
배열 값이 0인 경우와 탐색하지 않았을 경우 쿼리의 반환 값이 어떻게 되어야 하느냐를 잘 생각해보면 어렵지 않게 풀 수 있다. 다만 파이썬은 노드 값들을 모두 나눠서 저장하지 않으면 시간초과...
