
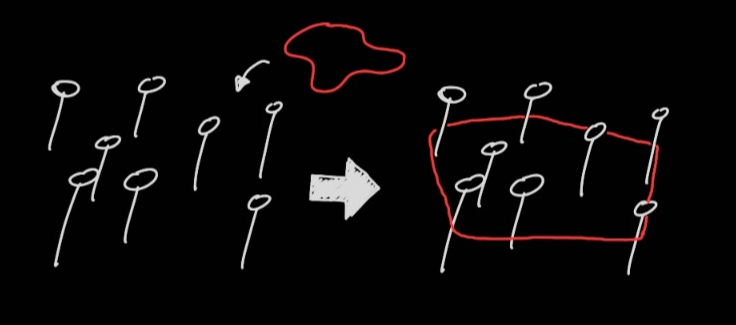
여러 객체가 주어졌을 때, 객체를 둘러싸는 껍질을 만드는 문제다. 적용되는 가장 직관적인 현상은 고무줄이다. 몇 개의 못을 박아두고 못을 전부 안쪽으로 감싸도록 고무줄을 걸어주면 고무줄이 만든 도형이 볼록껍질이 된다.
1. 문제상황
볼록껍질을 만드는 문제상황을 아래 그림을 예시로 생각해 보자. 평면상에 10개의 좌표가 주어져있고 이 점들을 감싸는 최소 면적의 볼록 다각형을 구성하는 점을 특정하는 것이 이 문제의 해가 된다.

해를 구할 수 있는 방법은 모든 점을 방문하며 확인해보는 방법도 있겠으나, 가장 널리 알려진 것은 O(NlogN)의 시간복잡도를 가진 그라함 스캔(Graham's scan)이다.
2. CCW(Counter Clock Wise) 알고리즘
그라함 스캔 알고리즘을 수행하기 위해서는 두 점으로 표현되는 벡터와 한 점의 위치 관계를 파악할 수 있어야 한다. 이 과정은 세 점을 순서대로 잇는 것으로 이해할 수 있다. 1, 2, 3번 점을 순서대로 이어갈 때, 1에서 2번 점을 이은 선분의 방향에서 2에서 3을 잇는 선분의 방향은 왼쪽, 오른쪽으로 꺾이는 경우와 같은 방향을 유지하는 세 가지 경우로 나뉜다. 이때 좌회전의 경우, 점을 계속해서 받아 이어나가면 결국 반시계방향으로 벡터의 방향이 바뀌므로 이를 판별하는 알고리즘을 CCW라고 부른다.
판별식은 벡터의 외적을 활용하며 단 한 줄의 연산으로 끝난다. P1 = (x1,y1), P2 = (x2,y2), P3 = (x3,y3)로 정의되는 세 점이 있을 때, P1-P2-P3 순으로 이어가는 선분은 다음 식에 따라 양수, 0, 음수의 결과를 내놓는다.
CCW(P1, P2, P3) = (y2-y1)×(x3-x2)-(x2-x1)×(y3-y2)
결과가 양수인 경우, 세 점은 반시계방향, 즉 좌회전하는 것이고, 0인 경우 같은 직선 상에 위치한 것이다. 음수인 경우는 시계방향, 즉 우회전하는 것이다.
3. 그라함 스캔
그라함 스캔을 적용하기 위해 먼저 좌표 값들을 사전에 정렬해야 한다. 이때 정렬은 x좌표, y좌표 값을 기준으로 하지 않고 한 점을 중심으로 방향에 따라 이루어진다.
정렬을 위한 기준점을 선정할 때 고려해야 할 점은 정렬 기준점이 반드시 볼록껍질에 포함되어야 한다는 것이다. 볼록 껍질을 바로 특정할 수는 없으나 볼록껍질에 포함되는 한 점을 찾는 좋은 방법이 있다. 하나의 직선을 두고 이 직선을 평행이동하며 가장 먼저 만나는 점을 찾는 것이다. 이 작업을 가장 쉽게 할 수 있는 직선은 x=a 또는 y=b이다. 따라서 기준점은 x나 y좌표값을 기준으로 가장 작거나 가장 큰 값을 갖는 점을 고를 수 있다.
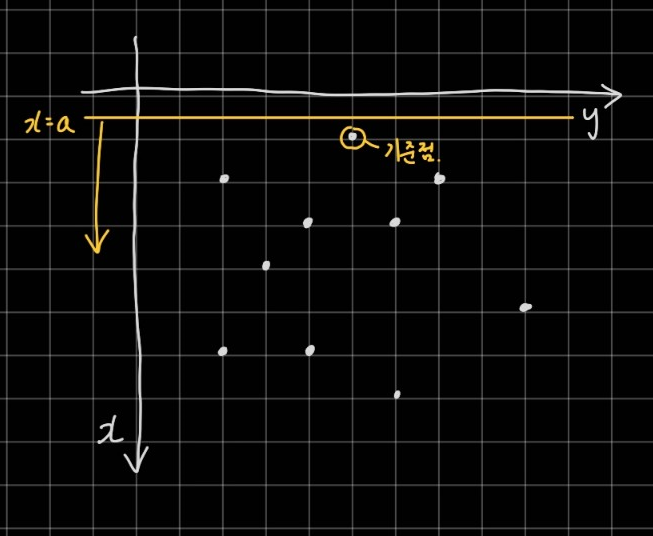
예시로 만든 문제상황에서는 x값이 가장 작은 점을 기준으로 정했다. 이 점은 가장 바깥쪽에 존재하며 이보다 더 x값이 작은 점이 없으므로 반드시 볼록껍질에 포함되는 점이다. 여기서부터 직선의 기울기를 바꿔가며 만나는 순서로 점을 정렬한다.
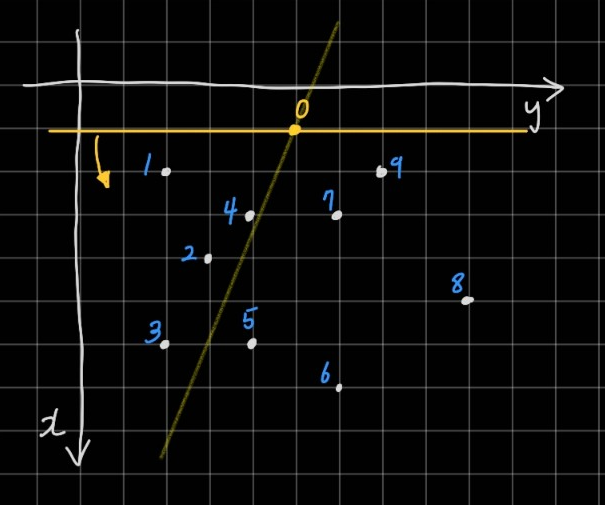
이렇게 기준을 0으로, 나머지 점들에 1~9까지의 번호가 매겨졌다. 이제 1번 점부터 방문하며 두 점을 잇는 직선을 만들어 나머지 점들의 위치가 한 곳으로 모여있는지, 나뉘어있는지를 판별한다.
여기서 사용되는 중요한 성질이 한 가지 있는데, 평면 상에 주어진 여러 점에서 두 개의 점을 골라 직선을 만들었을 때, 나머지 모든 점이 직선을 기준으로 한쪽에 모여있다면(직선 위에 있는 것은 양쪽에 존재하는 것으로 간주한다.) 그 직선은 반드시 볼록껍질을 구성하는 한 변을 포함한다. 따라서 기준점이 반드시 볼록껍질의 꼭짓점이므로 어떤 점과 이룬 직선이 나머지 점을 한쪽으로 몰아넣는다면 그 점 역시 볼록껍질에 포함되는 것이다.
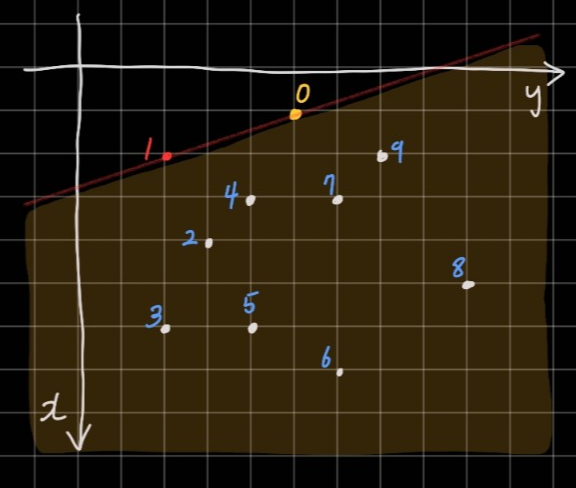
0번과 1번으로 만들어진 직선은 나머지 모든 점을 한 쪽으로 몰아넣었다. 그럼 1번은 볼록껍질에 포함되는 점이다. 다음 점인 2번은 가장 최근에 확인한 볼록껍질의 꼭짓점인 1번과 직선을 이루도록 한다.
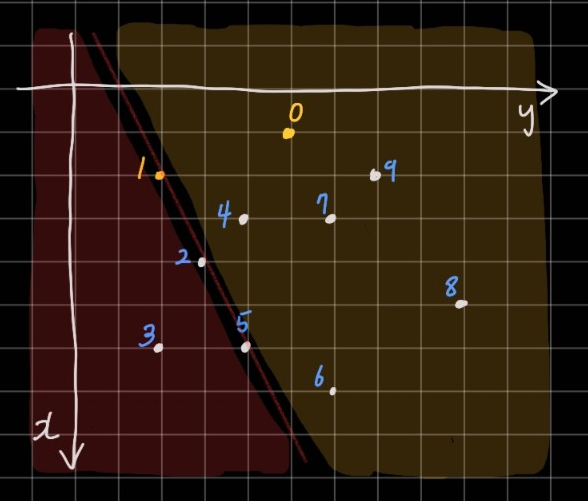
1번과 2번으로 만들어진 직선은 양쪽에 점을 나눠갖게 된다. 2번은 볼록껍질의 꼭짓점이 아니다. 그럼 2번을 넘어서 1번과 3번으로 직선을 만들어본다.
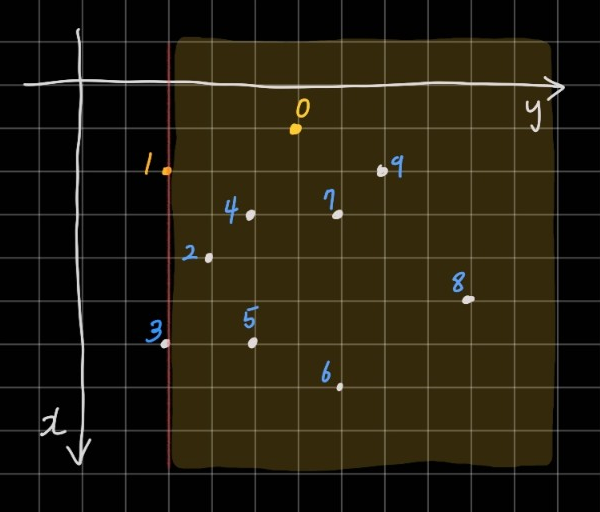
모든 점이 한 쪽으로 몰려있다. 3번 역시 볼록껍질의 꼭짓점이다.
직관적으로 이해하기 쉬운 그림으로 표현했지만 그라함 스캔의 정확한 과정에서는 한 점을 방문하고 다음 점으로 넘어갈 때, 직선이 꺾이는 방향이 바뀌는가 여부를 본다. 위 과정에 의하면 다음 점을 방문할 때, 볼록껍질이 만들어진다면 반드시 왼쪽에 있는 점들만 방문한다. 그런데 2번 점의 경우, 3번 점으로 넘어갈 때 오른쪽에 위치한 점을 가야 하므로 2번 점은 빠져야 하는 것이다.
이제 이 과정을 마지막 점까지 반복하고, 가장 마지막에 꼭짓점인 것으로 판정된 점과 시작점을 연결해주면 아래 그림과 같은 볼록껍질이 완성된다.
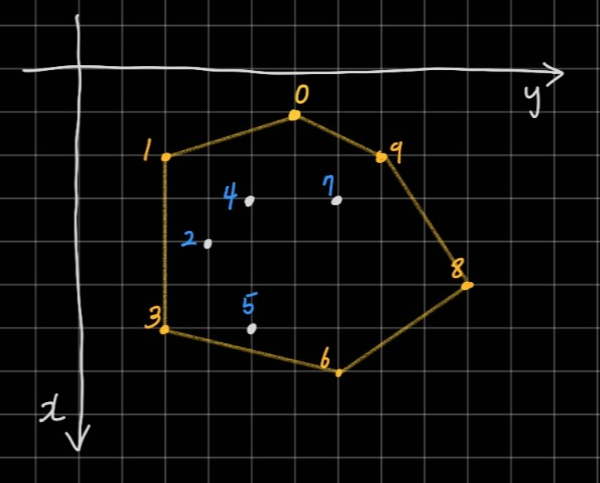
이 과정이 그라함 스캔이다. 단순해보이지만 구현해야 할 것이 많다.
4. 구현
그라함 스캔의 단계를 이렇게 정리할 수 있다.
- 기준점 정하기
- 나머지 점 정렬하기
- 점 순차적으로 방문하며 방향 확인하기
- 방향이 반대라면 점을 제거하고 다음 점 방문
- 마지막 점을 방문할 때 까지 반복
5. 소스코드
# 점의 좌표를 입력받음
N = int(input())
dot = [list(map(int,input().split())) for _ in range(N)]
# 세 점의 위치관계를 파악
def ccw(a, b, c):
k = (b[1]-a[1])*(c[0]-b[0])-(b[0]-a[0])*(c[1]-b[1])
if k > 0: return 1
elif k < 0: return -1
else: return 0
# 그라함 스캔
def graham(dots):
# 점의 순서를 x좌표를 우선으로 정렬
# 원래는 기준점을 중심으로 극좌표계 정렬을 해주어야 하지만
# 단순히 2차원 배열 정렬을 한 후, 정방향으로, 역방향으로 한차례씩 스캔해주면
# 왼쪽과 오른쪽의 볼록껍질이 만들어지고 이를 합치면
# 하나의 볼록껍질이 완성된다.
dots.sort()
# 왼쪽 볼록껍질 스캔
left = []
for p in dots:
while len(left) >= 2 and ccw(left[-2],left[-1],p) <= 0:
left.pop()
left.append(p)
# 오른쪽 볼록껍질 스캔
right = []
for p in reversed(dots):
while len(right) >= 2 and ccw(right[-2],right[-1],p) <= 0:
right.pop()
right.append(p)
# 양측 볼록껍질의 끝은 서로의 시작점과 겹치기 때문에 제거하여 반환
return left[:-1]+right[:-1]
print(*graham(dot))
