31434 당근 클릭 게임 (백준, python3)

시간 제한	메모리 제한
2초	1024MB

문제

에릭은 방학 동안 너무 심심한 나머지, 당근 클릭 게임이라는 게임을 직접 만들어서 플레이하기로 했다.

이 게임에서 초기에 에릭은 당근을 0개 가지고 있고, s가 1인 상태로 게임을 시작한다.
그 후, 매초 다음 두 가지의 행동 중 하나를 할 수 있다.

1. 마우스를 클릭하고 당근을 s개 얻는다.
2. 정수 i (1 ≤ i ≤ N)를 고르고, 당근 A_i개를 지불하여 i번째 스피드 효과를 구매한다. 구매 직후, s가 B_i만큼 증가한다. (이전에 구매한 스피드 효과를 다시 구매하는 것도 가능하다.)

게임을 개발하느라 에너지를 모두 소모해 버린 에릭을 위해 게임을 K초 플레이한 후 당근을 최대 몇 개까지 가지고 있을 수 있는지 알려주자!

입력

첫 번째 줄에 두 정수 N, K가 공백으로 구분되어 주어진다.
다음 N개의 줄 중 i번째 줄에 두 정수 A_i, B_i가 공백으로 구분되어 주어진다.

출력

에릭이 게임을 K초 플레이한 후 최대로 가지고 있을 수 있는 당근의 개수를 출력한다.

제한

• 1 ≤ N, K ≤ 100
• 1 ≤ Ai, Bi ≤ 50

서브태스크

번호	배점	제한
1	3	K ≤ 2
2	12	N ≤ 4, K ≤ 10
3	20	N = 1
4	65	추가 제약 조건 없음

---

풀이

오랜만에 풀어보는 DP문제! 점화식 감다뒤...

 

t초에 도달한 상태를 생각해보자. 여러 경우가 있을텐데 당근을 얻는 속도인 s가 1부터 존재할 수 있고, 각 s에 따라 t초에 가질 수 있는 당근의 양 c가 있다. 2차원 배열을 다음과 같이 선언해보자.

DP[시간 t][속도 s] = 당근 c

만약 이전 시간 t-1에서 당근 속도를 업그레이드 할 상품이 다양해 t시간에 속도 s에 도달할 방법이 여러 가지였다고 가정해보자. 이 경우, c가 가장 많은 경우만이 최적해에 가까이 갈 수 있다. 같은 시간, 같은 속도라면 당연히 당근이 많은 쪽이 더 많아질테니까.

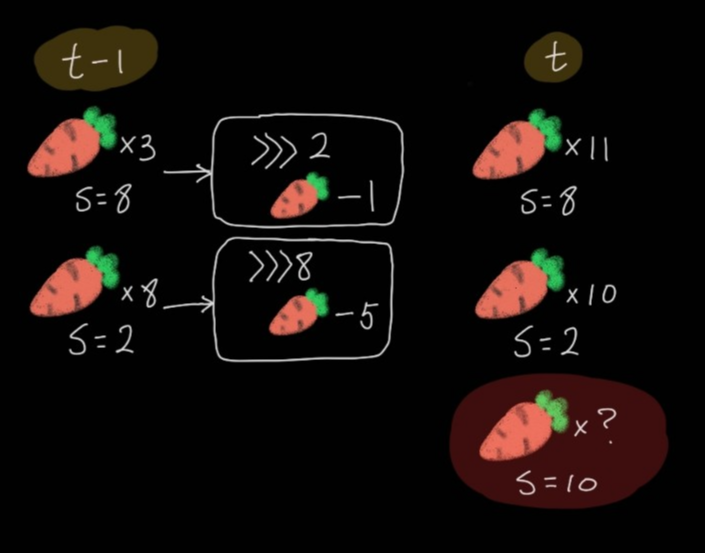
이런 경우, t-1 시점에서 당근이 3개 남은 쪽은 가격이 1인 업그레이드를, 8개 남은 쪽은 가격이 5인 업그레이드를 살 수 있다.

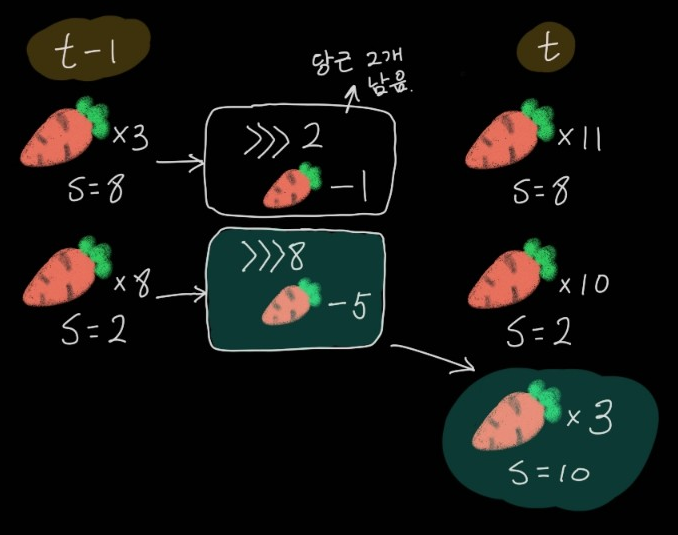
결과는 속도가 같다면 거스름돈이 많은 쪽만 남기는 것이다. 그럼 이제 점화식을 이렇게 생각할 수 있다.

A_i, B_i에 대하여
DP[t+1][s] = max(DP[t][s]+s, DP[t+1][s])
DP[t+1][s+B_i] = max(DP[t][s]-A_i, DP[t+1][s+B_i])

t를 0에서 K-1까지 탐색시키고 DP[K]의 모든 값 중 가장 큰 값 하나를 꺼내면 K초 후에 가지고 있을 수 있는 최대 당근의 수를 얻는다.

 

정답 코드

import sys
input = sys.stdin.readline

N,K = map(int,input().split())
store = [tuple(map(int,input().split())) for _ in range(N)]
store.sort() #여기서 정렬을 해주는 것이 구매 가능성을 따질 때 유리하다.

dp = [[-1 for _ in range(5001)] for _ in range(K+1)]
dp[0][1] = 0
highspeed = 1
for i in range(K):
    for j in range(1, highspeed+1):
        if dp[i+1][j] == -1 or dp[i+1][j] < dp[i][j]+j:
            dp[i+1][j] = dp[i][j] + j # 업그레이드를 구매하지 않고 당근을 얻는 경우
            for cost, increase in store:
                if cost > dp[i][j]: break # 업그레이드 가격이 현재 당근 수보다 많은 경우
                if dp[i+1][j+increase] == -1 or dp[i+1][j+increase] < dp[i][j]-cost:
                    dp[i+1][j+increase] = dp[i][j]-cost # 업그레이드 후 비교
                    if j+increase > highspeed:
                        highspeed = j+increase

maximum = 0
for k in dp[K]:
    if k > maximum:
        maximum = k

print(maximum)