
| 시간 제한 | 메모리 제한 |
| 1초 | 128MB |
문제
어떤 도시의 중심가는 N개의 동서방향 도로와 N개의 남북방향 도로로 구성되어 있다.
모든 도로에는 도로 번호가 있으며 남북방향 도로는 왼쪽부터 1에서 시작하여 N까지 번호가 할당되어 있고 동서방향 도로는 위부터 1에서 시작하여 N까지 번호가 할당되어 있다. 또한 동서방향 도로 사이의 거리와 남 북방향 도로 사이의 거리는 모두 1이다. 동서방향 도로와 남북방향 도로가 교차하는 교차로의 위치는 두 도로의 번호의 쌍인 (동서방향 도로 번호, 남북방향 도로 번호)로 나타낸다. N이 6인 경우의 예를 들면 다음과 같다.
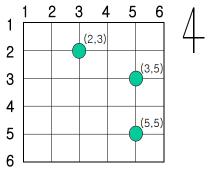
이 도시에는 두 대의 경찰차가 있으며 두 차를 경찰차1과 경찰차2로 부른다. 처음에는 항상 경찰차1은 (1, 1)의 위치에 있고 경찰차2는 (N, N)의 위치에 있다. 경찰 본부에서는 처리할 사건이 있으면 그 사건이 발생된 위치를 두 대의 경찰차 중 하나에 알려 주고, 연락 받은 경찰차는 그 위치로 가장 빠른 길을 통해 이동하여 사건을 처리한다. (하나의 사건은 한 대의 경찰차가 처리한다.) 그리고 사건을 처리 한 경찰차는 경찰 본부로부터 다음 연락이 올 때까지 처리한 사건이 발생한 위치에서 기다린다. 경찰 본부에서는 사건이 발생한 순서대로 두 대의 경찰차에 맡기려고 한다. 처리해야 될 사건들은 항상 교차로에서 발생하며 경찰 본부에서는 이러한 사건들을 나누어 두 대의 경찰차에 맡기되, 두 대의 경찰차들이 이동하는 거리의 합을 최소화 하도록 사건을 맡기려고 한다.
예를 들어 앞의 그림처럼 N=6인 경우, 처리해야 하는 사건들이 3개 있고 그 사건들이 발생된 위치 를 순서대로 (3, 5), (5, 5), (2, 3)이라고 하자. (3, 5)의 사건을 경찰차2에 맡기고 (5, 5)의 사건도 경찰차2에 맡기며, (2, 3)의 사건을 경찰차1에 맡기면 두 차가 이동한 거리의 합은 4 + 2 + 3 = 9가 되 고, 더 이상 줄일 수는 없다.
처리해야 할 사건들이 순서대로 주어질 때, 두 대의 경찰차가 이동하는 거리의 합을 최소화 하도록 사건들을 맡기는 프로그램을 작성하시오.
입력
첫째 줄에는 동서방향 도로의 개수를 나타내는 정수 N(5 ≤ N ≤ 1,000)이 주어진다. 둘째 줄에는 처리해야 하는 사건의 개수를 나타내는 정수 W(1 ≤ W ≤ 1,000)가 주어진다. 셋째 줄부터 (W+2)번째 줄까지 사건이 발생된 위치가 한 줄에 하나씩 주어진다. 경찰차들은 이 사건들을 주어진 순서대로 처리해야 한다. 각 위치는 동서방향 도로 번호를 나타내는 정수와 남북방향 도로 번호를 나타내는 정수로 주어지며 두 정수 사이에는 빈칸이 하나 있다. 두 사건이 발생한 위치가 같을 수 있다.
출력
첫째 줄에 두 경찰차가 이동한 총 거리를 출력한다. 둘째 줄부터 시작하여 (i+1)번째 줄에 i(1 ≤ i ≤ W)번째 사건이 맡겨진 경찰차 번호 1 또는 2를 출력한다.
풀이
보자마자 "어 DP다."

1차시도
경찰차1과 2가 i번째 사건에서 j번째 사건으로 이동하는 거리를 모두 계산해서(O(W2)) 1번 사건부터 W번 사건까지 쭉 돌아보는 식으로 짜보려 했다. 그러니까 예제 입력 1에서 경찰차1의 DP 테이블은 아래와 같이 구성된다.
| 0 | 6 | 8 | 4 |
| 0 | 2 | 3 | |
| 0 | 5 | ||
| 0 |
이런 식으로 짜놓고 k번째 사건을 처리한다고 했을 때, 1~k-1번 사건까지의 최단 거리를 참조하면서 거기에 이번 사건을 1번에게 넘길지 2번에게 넘길지를 결정하는 식이었다. 이게 잘 생각해보니 DP의 탈을 쓴 그리디였는데 문제는 '이번 사건을 1번이나 2번에게 넘겨준다고 한들 이전 사건에서 이번 사건으로 넘어온 것이 다음 사건에 최적해인 것이 보장이 되느냐'였다. 천천히 생각해보니 보장이 되지 않으므로 모든 경로의 값을 다 기억해두어야 한다는 문제가 생겼다. 여기서 모든 경로를 트리구조로 저장하면 21000 만큼 메모리를 잡아먹기 때문에 이 방법은 포기.
2차시도
다시 고민에 빠져있다가 문득 스친 생각. "모든 사건을 결국 다 거쳐야 하니 하나의 경로로 만들어지지 않을까?". 오 기똥찬 아이디어다. 20개의 사건이 들어온다면 경찰차 1과 2가 20개의 사건을 맡아 이걸 다 이어보면 경찰차 1과 2, 그리고 사이에 20개의 사건을 잇는 하나의 경로가 만들어진다. 그렇다면 경찰차 1에서 사건 20개를 돌아 경찰차 2로 가는 가장 짧은 경로를 찾는...
까지 왔다가 생각이 끊겼는데 그 이유는 경찰차 1과 2가 W개의 사건을 순서대로 맡아나가야 하기 때문이다. 그러면 W개의 사건을 한 줄로 이은 최단 경로는 사건 순서를 무시하게 된다. 아쉽지만 이 아이디어는 폐기.
3차시도
도저히 모르겠어서 구글 선생님들의 도움을 얻었다. 이 문제 for문으로만 해결한 사람들도 꽤 있던데 많은 풀이가 재귀를 적용한 DP를 제시하고 있었다.
우선 재귀함수를 선언하는데 여기서 DP값을 반환해낸다. 함수 내부에서는 상위 단계의 최적해를 얻기위해 다시 함수를 재귀호출한다. 이걸 반복하면 최하위 단계에서 상수 값을 얻고 이걸 순차적으로 반환해나가며 해를 얻을 수 있다.
점화식을 도출하는 과정을 이렇게 정리할 수 있다.
먼저 W*W 크기의 2차원 배열 dist를 선언한다. 이 배열에서 dist[i][j]를 경찰차 1이 i번째 사건을, 경찰차 2가 j번째 사건을 처리했을 때 앞으로 남은 사건을 해결하기 위한 최단 경로로 정한다. 그럼 dist[i][j]를 얻기 위해서는 그보다 더 다음의 사건을 해결한 경우의 최단 거리를 먼저 얻어야 한다. 이렇게 거꾸로 돌아가다보면 가장 끝에는 dist[W][j] 또는 dist[i][W]가 있게 되고 이는 모두 0이다. (마지막 사건을 해결했으니 앞으로 해결할 사건이 없다.)
이제 dist[i][j]를 얻는 방법을 순차적으로 생각해보자.
경1과 경2가 각각 i, j번째 사건 위치에 있으니 다음 사건은 i, j 중 큰 값에서 1을 더한 값이다. 따라서 다음 사건의 번호 next를 이렇게 얻을 수 있다.
next = max(i, j) + 1그럼 다음 사건을 경1 또는 경2가 맡는 두 가지 경우가 존재한다. 두 경우의 현재 위치에서 다음 사건까지의 거리를 각각 dist_i, dist_j라고 한다면 다음과 같이 얻을 수 있다. 여기서 case는 사건의 좌표를 저장한 배열이다.
def distance(a,b):
return abs(a[0]-b[0]) + abs(a[1]-b[1])
next = max(i, j) + 1
dist_i = distance(case[i],case[next])
dist_j = distance(case[j],case[next])
dist[i][j] = min(dist_i + dist[next][j], dist_j + dist[i][next])마지막 줄이 점화식이라고 볼 수 있다. 그런데 여기서 dist[i][j]를 구성하기 위한 dist[next][j]와 dist[i][next]는 dist[i][j]보다 먼저 구성되어있어야 한다. 따라서 이 점화식은 상향식으로 구성되어야 함을 알 수 있다. 여기서 재귀 함수가 필요하다. 이제 dist배열의 값을 재귀함수로 불러오도록 하기 위해 dp함수를 아래와 같이 구성한다. 무한 호출에 빠지지 않도록 탈출 조건은 i와 j가 W일 경우로 설정한다.
def distance(a,b):
return abs(a[0]-b[0]) + abs(a[1]-b[1])
def dp(i,j):
if i == W or j == W:
return 0
next = max(i, j) + 1
dist_i = distance(case[i],case[next])
dist_j = distance(case[j],case[next])
dist[i][j] = min(dist_i + dp(next,j), dist_j + dp(i,next))
return dist[i][j]이제 여기서 탐색한 dist[i][j]는 다시 호출해 계산할 필요가 없으니 초기값을 확인해 이미 채워진 경우라면 바로 값을 불러와 호출하도록 하고, i와 j가 0인 경우도 처리해준다.
def distance(a,b):
return abs(a[0]-b[0]) + abs(a[1]-b[1])
def dp(i,j):
if i == W or j == W:
return 0
if dist[i][j] == -1:
next = max(i, j) + 1
if i == 0:
dist_i = distance(case[i],[1,1])
else:
dist_i = distance(case[i],case[next])
if j == 0:
dist_j = distance(case[j],[N,N])
else:
dist_j = distance(case[j],case[next])
dist[i][j] = min(dist_i + dp(next,j), dist_j + dp(i,next))
return dist[i][j]완성이다. 이러면 상향식으로 값을 불러와 경1과 경2가 아직 사건을 하나도 해결하지 않은 dp(0,0)의 값으로 앞으로 남은 최적 경로의 거리를 얻을 수 있다. 그리고 이 값을 호출하는 과정에서 필요한 dist배열의 모든 값은 갱신되어있다. 그럼 이걸 이용해 각 사건을 경1과 경2 중 누가 해결하는지 찾아보자.
재귀호출을 이용한 dfs로 구현했다. dist[0][0] 시점에서 다음 사건으로 경1 또는 경2가 이어지는 거리가 각각 dist_i, dist_j라고 했다. 그럼 두 경우를 모두 확인해 dist 배열 상에 저장된 값으로 계산하여 값이 더 작은 쪽을 선택하는 것이 최적 경로다. 이게 처음 탐색하는 것이라면 보장이 안되지만 dist 배열은 이미 계산이 끝나있기 때문에 이렇게만 따라가도 된다. O(W)이다.
def path(i,j):
if i == W or j == W:
return
dist_i, dist_j, next = 0, 0, max(i,j) + 1
if i == 0:
dist_i = distance(case[next], [1,1])
else:
dist_i = distance(case[next], case[i])
if j == 0:
dist_j = distance(case[next], [N,N])
else:
dist_j = distance(case[next], case[j])
# 다음 사건을 경1 또는 경2가 해결할 때 남은 거리를 각각 비교
if dist[next][j] + dist_i < dist[i][next] + dist_j:
print(1)
path(next,j)
else:
print(2)
path(i,next)아 그리고 재귀호출의 깊이가 1000까지 가는데 이게 백준 채점 서버에서 걸어둔 리미트에 딱 걸린다. 그래서 이걸 해제해줘야 한다.
import sys
sys.setrecursionlimit(10**5)
정답 코드
import sys
sys.setrecursionlimit(10**5)
input = sys.stdin.readline
N = int(input())
W = int(input())
case = [[1,1]]+[list(map(int,input().split())) for _ in range(W)]
dist = [[-1 for _ in range(W+1)] for _ in range(W+1)]
def distance(a,b):
return abs(a[0]-b[0])+abs(a[1]-b[1])
def dp(i,j):
if i == W or j == W:
return 0
if dist[i][j] == -1:
dist_i,dist_j,next = 0,0,max(i,j)+1
if i == 0:
dist_i = distance(case[next],[1,1])
else:
dist_i = distance(case[next],case[i])
if j == 0:
dist_j = distance(case[next],[N,N])
else:
dist_j = distance(case[next],case[j])
dist_i += dp(next,j)
dist_j += dp(i,next)
if dist_i < dist_j:
dist[i][j] = dist_i
else:
dist[i][j] = dist_j
return dist[i][j]
def path(i,j):
if i == W or j == W:
return
dist_i,dist_j,next = 0,0,max(i,j)+1
if i == 0:
dist_i = distance(case[next],[1,1])
else:
dist_i = distance(case[next],case[i])
if j == 0:
dist_j = distance(case[next],[N,N])
else:
dist_j = distance(case[next],case[j])
if dist[next][j] + dist_i < dist[i][next] + dist_j:
print(1)
path(next,j)
else:
print(2)
path(i,next)
dp(0,0)
print(dist[0][0])
path(0,0)

| 시간 제한 | 메모리 제한 |
| 1초 | 128MB |
문제
어떤 도시의 중심가는 N개의 동서방향 도로와 N개의 남북방향 도로로 구성되어 있다.
모든 도로에는 도로 번호가 있으며 남북방향 도로는 왼쪽부터 1에서 시작하여 N까지 번호가 할당되어 있고 동서방향 도로는 위부터 1에서 시작하여 N까지 번호가 할당되어 있다. 또한 동서방향 도로 사이의 거리와 남 북방향 도로 사이의 거리는 모두 1이다. 동서방향 도로와 남북방향 도로가 교차하는 교차로의 위치는 두 도로의 번호의 쌍인 (동서방향 도로 번호, 남북방향 도로 번호)로 나타낸다. N이 6인 경우의 예를 들면 다음과 같다.

이 도시에는 두 대의 경찰차가 있으며 두 차를 경찰차1과 경찰차2로 부른다. 처음에는 항상 경찰차1은 (1, 1)의 위치에 있고 경찰차2는 (N, N)의 위치에 있다. 경찰 본부에서는 처리할 사건이 있으면 그 사건이 발생된 위치를 두 대의 경찰차 중 하나에 알려 주고, 연락 받은 경찰차는 그 위치로 가장 빠른 길을 통해 이동하여 사건을 처리한다. (하나의 사건은 한 대의 경찰차가 처리한다.) 그리고 사건을 처리 한 경찰차는 경찰 본부로부터 다음 연락이 올 때까지 처리한 사건이 발생한 위치에서 기다린다. 경찰 본부에서는 사건이 발생한 순서대로 두 대의 경찰차에 맡기려고 한다. 처리해야 될 사건들은 항상 교차로에서 발생하며 경찰 본부에서는 이러한 사건들을 나누어 두 대의 경찰차에 맡기되, 두 대의 경찰차들이 이동하는 거리의 합을 최소화 하도록 사건을 맡기려고 한다.
예를 들어 앞의 그림처럼 N=6인 경우, 처리해야 하는 사건들이 3개 있고 그 사건들이 발생된 위치 를 순서대로 (3, 5), (5, 5), (2, 3)이라고 하자. (3, 5)의 사건을 경찰차2에 맡기고 (5, 5)의 사건도 경찰차2에 맡기며, (2, 3)의 사건을 경찰차1에 맡기면 두 차가 이동한 거리의 합은 4 + 2 + 3 = 9가 되 고, 더 이상 줄일 수는 없다.
처리해야 할 사건들이 순서대로 주어질 때, 두 대의 경찰차가 이동하는 거리의 합을 최소화 하도록 사건들을 맡기는 프로그램을 작성하시오.
입력
첫째 줄에는 동서방향 도로의 개수를 나타내는 정수 N(5 ≤ N ≤ 1,000)이 주어진다. 둘째 줄에는 처리해야 하는 사건의 개수를 나타내는 정수 W(1 ≤ W ≤ 1,000)가 주어진다. 셋째 줄부터 (W+2)번째 줄까지 사건이 발생된 위치가 한 줄에 하나씩 주어진다. 경찰차들은 이 사건들을 주어진 순서대로 처리해야 한다. 각 위치는 동서방향 도로 번호를 나타내는 정수와 남북방향 도로 번호를 나타내는 정수로 주어지며 두 정수 사이에는 빈칸이 하나 있다. 두 사건이 발생한 위치가 같을 수 있다.
출력
첫째 줄에 두 경찰차가 이동한 총 거리를 출력한다. 둘째 줄부터 시작하여 (i+1)번째 줄에 i(1 ≤ i ≤ W)번째 사건이 맡겨진 경찰차 번호 1 또는 2를 출력한다.
풀이
보자마자 "어 DP다."

1차시도
경찰차1과 2가 i번째 사건에서 j번째 사건으로 이동하는 거리를 모두 계산해서(O(W2)) 1번 사건부터 W번 사건까지 쭉 돌아보는 식으로 짜보려 했다. 그러니까 예제 입력 1에서 경찰차1의 DP 테이블은 아래와 같이 구성된다.
| 0 | 6 | 8 | 4 |
| 0 | 2 | 3 | |
| 0 | 5 | ||
| 0 |
이런 식으로 짜놓고 k번째 사건을 처리한다고 했을 때, 1~k-1번 사건까지의 최단 거리를 참조하면서 거기에 이번 사건을 1번에게 넘길지 2번에게 넘길지를 결정하는 식이었다. 이게 잘 생각해보니 DP의 탈을 쓴 그리디였는데 문제는 '이번 사건을 1번이나 2번에게 넘겨준다고 한들 이전 사건에서 이번 사건으로 넘어온 것이 다음 사건에 최적해인 것이 보장이 되느냐'였다. 천천히 생각해보니 보장이 되지 않으므로 모든 경로의 값을 다 기억해두어야 한다는 문제가 생겼다. 여기서 모든 경로를 트리구조로 저장하면 21000 만큼 메모리를 잡아먹기 때문에 이 방법은 포기.
2차시도
다시 고민에 빠져있다가 문득 스친 생각. "모든 사건을 결국 다 거쳐야 하니 하나의 경로로 만들어지지 않을까?". 오 기똥찬 아이디어다. 20개의 사건이 들어온다면 경찰차 1과 2가 20개의 사건을 맡아 이걸 다 이어보면 경찰차 1과 2, 그리고 사이에 20개의 사건을 잇는 하나의 경로가 만들어진다. 그렇다면 경찰차 1에서 사건 20개를 돌아 경찰차 2로 가는 가장 짧은 경로를 찾는...
까지 왔다가 생각이 끊겼는데 그 이유는 경찰차 1과 2가 W개의 사건을 순서대로 맡아나가야 하기 때문이다. 그러면 W개의 사건을 한 줄로 이은 최단 경로는 사건 순서를 무시하게 된다. 아쉽지만 이 아이디어는 폐기.
3차시도
도저히 모르겠어서 구글 선생님들의 도움을 얻었다. 이 문제 for문으로만 해결한 사람들도 꽤 있던데 많은 풀이가 재귀를 적용한 DP를 제시하고 있었다.
우선 재귀함수를 선언하는데 여기서 DP값을 반환해낸다. 함수 내부에서는 상위 단계의 최적해를 얻기위해 다시 함수를 재귀호출한다. 이걸 반복하면 최하위 단계에서 상수 값을 얻고 이걸 순차적으로 반환해나가며 해를 얻을 수 있다.
점화식을 도출하는 과정을 이렇게 정리할 수 있다.
먼저 W*W 크기의 2차원 배열 dist를 선언한다. 이 배열에서 dist[i][j]를 경찰차 1이 i번째 사건을, 경찰차 2가 j번째 사건을 처리했을 때 앞으로 남은 사건을 해결하기 위한 최단 경로로 정한다. 그럼 dist[i][j]를 얻기 위해서는 그보다 더 다음의 사건을 해결한 경우의 최단 거리를 먼저 얻어야 한다. 이렇게 거꾸로 돌아가다보면 가장 끝에는 dist[W][j] 또는 dist[i][W]가 있게 되고 이는 모두 0이다. (마지막 사건을 해결했으니 앞으로 해결할 사건이 없다.)
이제 dist[i][j]를 얻는 방법을 순차적으로 생각해보자.
경1과 경2가 각각 i, j번째 사건 위치에 있으니 다음 사건은 i, j 중 큰 값에서 1을 더한 값이다. 따라서 다음 사건의 번호 next를 이렇게 얻을 수 있다.
next = max(i, j) + 1그럼 다음 사건을 경1 또는 경2가 맡는 두 가지 경우가 존재한다. 두 경우의 현재 위치에서 다음 사건까지의 거리를 각각 dist_i, dist_j라고 한다면 다음과 같이 얻을 수 있다. 여기서 case는 사건의 좌표를 저장한 배열이다.
def distance(a,b):
return abs(a[0]-b[0]) + abs(a[1]-b[1])
next = max(i, j) + 1
dist_i = distance(case[i],case[next])
dist_j = distance(case[j],case[next])
dist[i][j] = min(dist_i + dist[next][j], dist_j + dist[i][next])마지막 줄이 점화식이라고 볼 수 있다. 그런데 여기서 dist[i][j]를 구성하기 위한 dist[next][j]와 dist[i][next]는 dist[i][j]보다 먼저 구성되어있어야 한다. 따라서 이 점화식은 상향식으로 구성되어야 함을 알 수 있다. 여기서 재귀 함수가 필요하다. 이제 dist배열의 값을 재귀함수로 불러오도록 하기 위해 dp함수를 아래와 같이 구성한다. 무한 호출에 빠지지 않도록 탈출 조건은 i와 j가 W일 경우로 설정한다.
def distance(a,b):
return abs(a[0]-b[0]) + abs(a[1]-b[1])
def dp(i,j):
if i == W or j == W:
return 0
next = max(i, j) + 1
dist_i = distance(case[i],case[next])
dist_j = distance(case[j],case[next])
dist[i][j] = min(dist_i + dp(next,j), dist_j + dp(i,next))
return dist[i][j]이제 여기서 탐색한 dist[i][j]는 다시 호출해 계산할 필요가 없으니 초기값을 확인해 이미 채워진 경우라면 바로 값을 불러와 호출하도록 하고, i와 j가 0인 경우도 처리해준다.
def distance(a,b):
return abs(a[0]-b[0]) + abs(a[1]-b[1])
def dp(i,j):
if i == W or j == W:
return 0
if dist[i][j] == -1:
next = max(i, j) + 1
if i == 0:
dist_i = distance(case[i],[1,1])
else:
dist_i = distance(case[i],case[next])
if j == 0:
dist_j = distance(case[j],[N,N])
else:
dist_j = distance(case[j],case[next])
dist[i][j] = min(dist_i + dp(next,j), dist_j + dp(i,next))
return dist[i][j]완성이다. 이러면 상향식으로 값을 불러와 경1과 경2가 아직 사건을 하나도 해결하지 않은 dp(0,0)의 값으로 앞으로 남은 최적 경로의 거리를 얻을 수 있다. 그리고 이 값을 호출하는 과정에서 필요한 dist배열의 모든 값은 갱신되어있다. 그럼 이걸 이용해 각 사건을 경1과 경2 중 누가 해결하는지 찾아보자.
재귀호출을 이용한 dfs로 구현했다. dist[0][0] 시점에서 다음 사건으로 경1 또는 경2가 이어지는 거리가 각각 dist_i, dist_j라고 했다. 그럼 두 경우를 모두 확인해 dist 배열 상에 저장된 값으로 계산하여 값이 더 작은 쪽을 선택하는 것이 최적 경로다. 이게 처음 탐색하는 것이라면 보장이 안되지만 dist 배열은 이미 계산이 끝나있기 때문에 이렇게만 따라가도 된다. O(W)이다.
def path(i,j):
if i == W or j == W:
return
dist_i, dist_j, next = 0, 0, max(i,j) + 1
if i == 0:
dist_i = distance(case[next], [1,1])
else:
dist_i = distance(case[next], case[i])
if j == 0:
dist_j = distance(case[next], [N,N])
else:
dist_j = distance(case[next], case[j])
# 다음 사건을 경1 또는 경2가 해결할 때 남은 거리를 각각 비교
if dist[next][j] + dist_i < dist[i][next] + dist_j:
print(1)
path(next,j)
else:
print(2)
path(i,next)아 그리고 재귀호출의 깊이가 1000까지 가는데 이게 백준 채점 서버에서 걸어둔 리미트에 딱 걸린다. 그래서 이걸 해제해줘야 한다.
import sys
sys.setrecursionlimit(10**5)
정답 코드
import sys
sys.setrecursionlimit(10**5)
input = sys.stdin.readline
N = int(input())
W = int(input())
case = [[1,1]]+[list(map(int,input().split())) for _ in range(W)]
dist = [[-1 for _ in range(W+1)] for _ in range(W+1)]
def distance(a,b):
return abs(a[0]-b[0])+abs(a[1]-b[1])
def dp(i,j):
if i == W or j == W:
return 0
if dist[i][j] == -1:
dist_i,dist_j,next = 0,0,max(i,j)+1
if i == 0:
dist_i = distance(case[next],[1,1])
else:
dist_i = distance(case[next],case[i])
if j == 0:
dist_j = distance(case[next],[N,N])
else:
dist_j = distance(case[next],case[j])
dist_i += dp(next,j)
dist_j += dp(i,next)
if dist_i < dist_j:
dist[i][j] = dist_i
else:
dist[i][j] = dist_j
return dist[i][j]
def path(i,j):
if i == W or j == W:
return
dist_i,dist_j,next = 0,0,max(i,j)+1
if i == 0:
dist_i = distance(case[next],[1,1])
else:
dist_i = distance(case[next],case[i])
if j == 0:
dist_j = distance(case[next],[N,N])
else:
dist_j = distance(case[next],case[j])
if dist[next][j] + dist_i < dist[i][next] + dist_j:
print(1)
path(next,j)
else:
print(2)
path(i,next)
dp(0,0)
print(dist[0][0])
path(0,0)
