어떤 그래프에서 정점을 제거했을 때, 그래프가 분리되어버리는 경우가 있습니다. 또는 간선을 제거 했을 때 분리되는 경우도 있습니다. 각각의 정점과 간선을 "단절점", "단절선"이라고 합니다.
1. 단절점의 특징
단절점과 단절선이 갖는 중요한 특징이 있습니다. 하나의 연결그래프를 dfs로 탐색하면 탐색 경로가 트리의 형태로 남게 됩니다. 여기서 어떤 정점 n을 탐색했을 때 그 정점으로부터 탐색된 하위 정점들에서 n의 상위 정점으로 돌아가는 경로가 하나도 없다면 n은 단절점이 됩니다. 그러니까, n을 제거하면 그보다 하위에 있는 모든 정점들은 n보다 상위 정점에서 분리되어버립니다. 돌아가는 길이 없으니까요. 이거 뭔가 지난 번에 정리한 SCC와 비슷한 느낌인데, 단절점을 찾는 과정이 SCC의 일부이기 때문입니다.
2. 단절점 탐색 과정
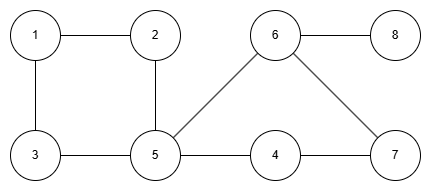
1에서 dfs 탐색을 출발해볼게요.
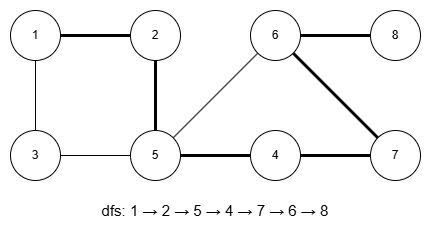
일단 순서대로 이렇게 탐색이 됩니다. 8에서 이제 탐색 가능한 간선을 찾다보면 6번을 찾을텐데 이미 탐색한 정점입니다. 이렇게 이미 탐색한 정점으로 돌아갈 수 있는 곳을 확인하면서 탐색을 되돌아올 때, 돌아갈 수 있으면서 탐색 순서가 가장 빠른 정점을 되돌려줍니다.
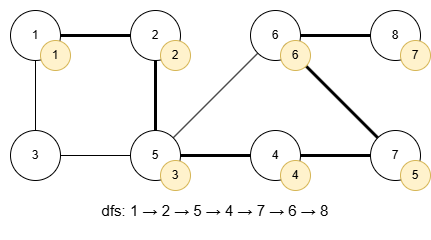
탐색 순서를 노란 원에 따로 넣었습니다. 이제 탈출할 때, 탐색에서 확인한 가장 빠른 탐색 순서를 반환하며 탈출합니다. 먼저 8은 7번째로 탐색된 정점이고 여기서 더 이상 확인할 정점이 없습니다. 다만, 연결된 정점 중 탐색 번호가 가장 빠른 건 이전 정점인 6입니다. 따라서 6의 탐색 순서인 6번을 반환하며 탈출합니다.
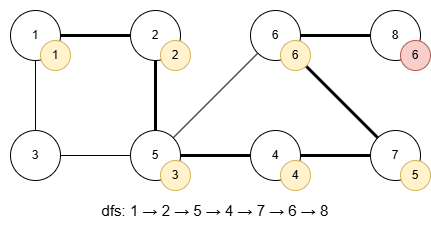
6에서 하위 탐색의 결과로 6번을 받았습니다. 이게 지금 자신의 탐색 순서와 같습니다. 이 경우, 하위 노드에서 6번보다 앞서 탐색되는 다른 정점으로 갈 수 있는 경로가 존재하지 않았음을 의미합니다. 그렇다면 이 정점을 끊어버리면 그래프가 분리됩니다. 이 정점을 단절점이라고 할 수 있습니다. 이어서 탐색을 해볼까요.
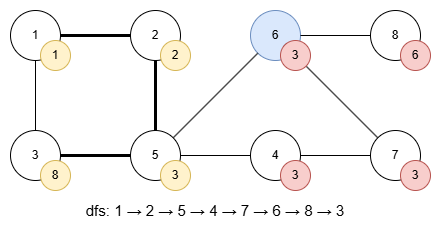
정점 6에서는 정점 5로 되돌아가는 간선이 있습니다. 그러므로 되돌아갈 수 있는 가장 빠른 탐색 번호가 3번으로 바뀌고 이걸 전달합니다. 정점 5는 4에서 돌아오는 3번이 자신의 탐색 번호와 같으니 단절점이 됩니다. 이어서 정점 3을 8번째로 탐색합니다.
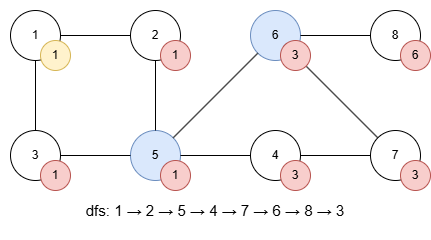
정점 3은 정점 1로 돌아갈 수 있으니 되돌아갈 수 있는 가장 빠른 탐색 번호를 1번으로 탈출합니다. 5, 2 순으로 탈출되고 1로 돌아옵니다. 여기서, 2에서 반환된 탐색 번호가 1번으로 자신과 같더라도 탐색의 출발점이었던 정점 1은 단절점이 될 수 없습니다. 출발 정점의 단절점 조건은 dfs에서 이어서 탐색된 하위 정점이 2개 이상인 것입니다. 여기서는 탐색된 하위 정점이 정점 2 뿐이므로 단절점이 아닙니다.
3. 원리
이 과정은 그래프에 대한 dfs의 결과가 항상 스패닝 트리임을 이용한 것입니다.
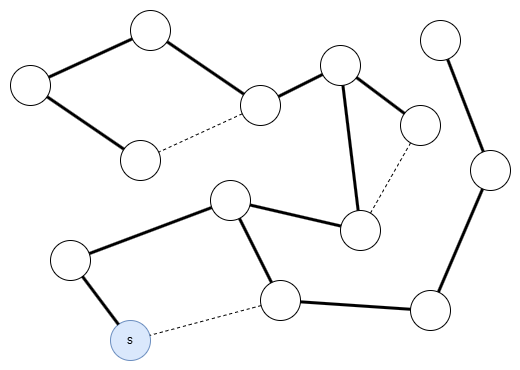
보시는 바와 같이 어떤 그래프도 연결그래프라는 것이 보장된다면 dfs로 탐색한 경로는 트리의 형태를 보입니다. 여기서 제거했을 때 그래프가 분리되는 정점들이 갖는 특징은 그 정점으로부터 이어진 탐색 간선이 모두 별개의 서브트리가 된다는 것입니다.
...
뭔가 더 근본적인 설명이 있을 것 같지만 수학적 지식이 모자라 이런 개떡같은 설명만 가능합니다...
4. 소스코드
check = [0] * (n + 1) # 탐색 여부를 관리합니다.
dfs_count = 1 # 현재 탐색 번호
articulation_point = set() # 단절점을 저장합니다.
s = 1 # 탐색을 시작할 정점의 번호
root_count = 0 # 출발 지점의 하위 탐색 정점 개수
def dfs(now):
global dfs_count
check[now] = dfs_count
near = dfs_count
dfs_count += 1
for next in graph[now]:
# 탐색 번호가 더 빠른 정점으로 돌아갈 수 있는지 확인
if check[next] and near > check[next]:
near = check[next]
# 탐색한 적 없는 정점이 있는 경우
elif check[next] == 0:
# 출발 정점의 하위 정점인 경우
if now == s:
global root_count
root_count += 1
sub = dfs(next) # 하위 정점으로 출발한 탐색에서
# 탐색 번호가 가장 빠른 정점을 찾습니다.
# 탐색 번호가 더 빠른 정점으로 연결되는 경우
if check[now] > sub:
near = min(near, sub)
# 탐색결과 돌아갈 수 있는 가장 빠른 탐색 번호가
# 자기 자신이거나 그보다 나중 정점인 경우
# 단절점이 되는 것으로 판정
else:
if now != s:
articulation_point.add(now)
return near
dfs(1)
# 탐색의 출발 정점의 하위 탐색 정점이 1개 보다 많으면
# 출발 정점이 단절점이 됩니다.
if root_count > 1:
articulation_point.add(s)
print(articulation_point)
5. 관련문제
