https://www.acmicpc.net/problem/11781

| 시간 제한 | 메모리 제한 |
| 1초 | 256MB |
문제
엔지니어의 행복도는 퇴근 후 집에 도착하는 시각이 늦을수록 낮아진다는 것이 증명되었다.
조이의 대표 레드는 엔지니어의 행복도를 최대한 높여야 할 의무가 있기 때문에, 신중하게 퇴근 시간을 조정하기로 하였다.
하지만 퇴근 시간을 조정하려면 먼저 엔지니어들이 집에 도착하는 시간을 알아야만 했다.
이 문제를 미카에게 맡기려고 했지만, 6시가 넘어 미카는 이미 퇴근해버렸기 때문에 레드는 고민에 빠지고 말았다.
레드를 도와 레드와 조이 엔지니어 모두의 행복도를 높여보도록 하자!
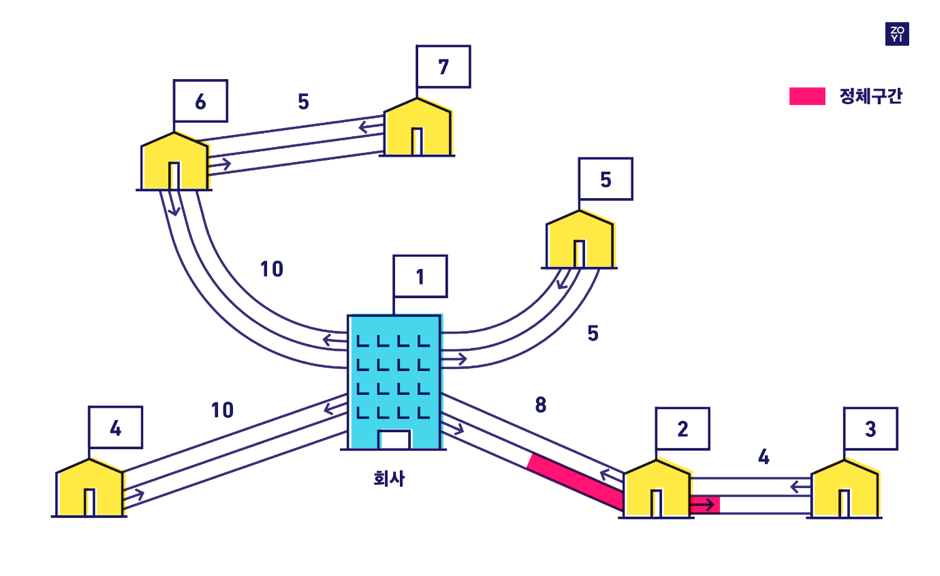
회사가 있는 서울은 N개의 지점으로 되어있다.
각 지점은 1번부터 N번의 번호를 가지고 있고, 회사는 1번 지점에 있다.
M개의 도로들은 서로 다른 지점을 연결하고 있으며, 임의의 지점에서 모든 지점으로 이동할 수 있다.
각각의 도로는 길이를 가지고 있으며, 거리 1을 이동하는 데 1분이 걸린다.
편의상 퇴근은 0분에 한다고 가정한다.
서울은 퇴근 시간에 도로가 막힌다.
퇴근 시간이 아닐 때에는 거리 1을 이동하는 데 1분이 걸리지만,
퇴근 시간이 겹칠 경우 혼잡한 도로는 거리 1을 이동하는 데 2분이 걸리게 된다. (물론 퇴근 시간에 막히지 않는 도로도 있다.)
만약 퇴근 시간이 10분부터 20분이고 어떤 도로에 진입한 순간이 15분이며, 도로의 길이는 10이라면 이 도로를 전부 통과하는 데 걸리는 시간은
- 퇴근 시간 : 5분(15 ~ 20분)동안 간 거리 = 2.5를 가는 데 걸린 시간 : 5분
- 퇴근 시간 외의 시간 : 나머지 거리 7.5를 가는 데 걸린 시간 : 7.5분
총 12.5분이 된다.
입력
첫째 줄에는 N, M과 퇴근 시간의 시작과 끝을 의미하는 S와 E가 정수로 주어진다. (2 ≤ N ≤ 5,000, 1 ≤ M ≤ 100,000, 0 ≤ S < E ≤ 1,000,000,000)
다음 M개의 줄에는 서로 다른 정수 A, B와 도로의 길이를 의미하는 L, 그리고 t1, t2가 주어진다. (1 ≤ A, B ≤ N, 1 ≤ L ≤ 1,000,000,000, t1, t2 = 0 또는 1)
t1, t2는 A,B 사이에 퇴근 시간에 도로가 정체되는지 여부이다.
- t1 = 1 일 때는 퇴근 시간에 A에서 B로 이동시 정체됨을 의미하며,
- t2 = 1 일 때는 퇴근 시간에 B에서 A로 이동시 정체됨을 의미한다.
- 만약 t1 혹은 t2가 0이라면 각각의 이동시 정체되지 않음을 의미한다.
퇴근할 때는 같은 길로는 2번 이상 이동하지 않는다. 사원들은 언제나 최대한 빨리 집에 가고 싶어하기 때문에 일부러 늦는 길을 선택하지 않는다. 또한 이동할 때 멈추지 않고 계속 이동한다.
출력
모든 지점에 대해서 회사에서 출발했을 때 가장 늦게 도착하게 되는 지점까지의 도착 시각을 첫째 줄에 출력하라.
풀이
모든 정점을 다 탐색해보기 전에는 가장 오래 걸리는 탐색이 무엇인지 알 수 없기 때문에 최대 5,000개의 정점을 전부 탐색해야 합니다. 다행히 간선의 수도 100,000으로 그리 크지 않아서 충분히 시간 내에 다 돌아볼 수 있습니다.
그런데 정점 간의 거리는 주어지긴 하지만 퇴근 시간의 정체 여부가 도로마다 다르기도 하고, 퇴근시간을 걸쳐서 가는 경우와 그렇지 않은 경우도 있으므로 단순 거리만으로 탐색을 시도하면 안됩니다. 여기서는 거리가 아닌 이동 시간을 저장해가면서 가장 이동시간이 짧은 탐색을 꺼내 다음 탐색을 시도해야 합니다. 따라서 우선순위 큐가 필요합니다.
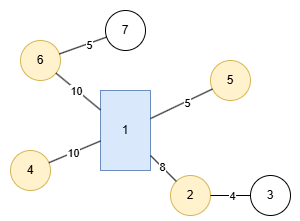
예제 입력1의 탐색을 직접 그려볼게요. 1번에서 탐색을 시작합니다. 다음으로 탐색되는 지점은 2, 4, 5, 6번 지점입니다. 각 지점까지의 도착 시간을 보면
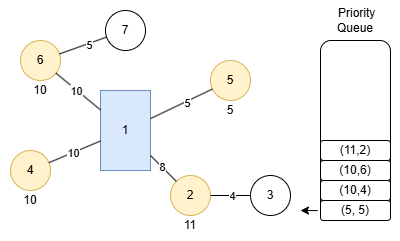
이렇게 됩니다. 1에서 4, 6으로 각각 이동하는 경우는 퇴근시간이 걸리지만 이 도로는 정체되지 않는다고 되어있으므로 이동 시간이 거리에 그대로 비례합니다. 그럼 이 도착 시간에 따라 다음으로 탐색되어야 하는 지점은 5번 지점입니다. 우선순위 큐에서 이게 가장 먼저 나오려면 각 지점에 도착한 시간을 키 값으로 enqueue해주어야 합니다.
만약 1에서 4로 이동하는 길이 정체되는 구간이라면 걸리는 시간은 어떻게 될까요?
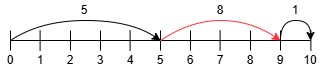
보시는 것처럼 거리 5까지는 누적 시간이 5이기 때문에 정체가 시작되지 않습니다. 그런데 그 다음으로부터 8의 시간동안이 퇴근 시간이므로 4의 거리만 이동할 수 있습니다. 나머지 1의 거리는 퇴근 시간이 지났으니 1의 시간으로 이동, 총 14의 시간이 소모됩니다.
따라서 우선순위 큐에서 지점의 도착 정보를 꺼내왔을 때, 그 시간이 그 지점에 도착하는 가장 빠른 시간이 됩니다. 이후로는 그 지점에 대한 탐색을 시도하지 않아도 됩니다. 다음 지점까지의 이동할 때 정체가 되는 구간을 지나야 한다면 경우의 수는 다음과 같습니다.
- 현재 퇴근 시간이 시작되기 전
- 이 구간을 통과해도 퇴근 시간이 시작되지 않음: 그냥 거리를 더해서 다음 시간을 구함
- 이 구간 내에서 퇴근 시간이 시작 됨
- 이 구간 내에서 퇴근 시간이 끝나지 않음: 퇴근 시간이 되기 전까지의 거리를 먼저 더하고, 남은 거리의 2배를 더해 다음 시간을 구함
- 이 구간 내에서 퇴근 시간이 끝남: 남은 퇴근 시간을 더하고 그 절반 만큼을 남은 거리에서 뺀 후 남은 거리를 더해 다음 시간을 구함
- 현재 퇴근 시간이 시작 됨
- 이 구간 내에서 퇴근 시간이 끝나지 않음: 구간 거리의 2배를 더해서 다음 시간을 구함
- 이 구간 내에서 퇴근 시간이 끝남: 남은 퇴근 시간을 더하고 그 절반 만큼을 남은 거리에서 뺀 후 남은 거리를 더해 다음 시간을 구함
- 현재 퇴근 시간이 지났음: 남은 거리를 더해 다음 시간을 구함
이렇게 모든 지점에 대해 가장 빠른 도달 시간을 구한 후에 가장 큰 값을 출력하도록 하면 되겠습니다.
정답 코드
import sys
from heapq import heappush, heappop
input = sys.stdin.readline
def solution():
n, m, s, e = map(int, input().split())
road = [dict() for _ in range(n + 1)]
inf = int(1e15)
check = [inf] * (n + 1)
for _ in range(m):
a, b, l, t1, t2 = map(int, input().split())
road[a][b] = (l, t1)
road[b][a] = (l, t2)
check[0] = check[1] = 0
hq = []
heappush(hq, (0, 1))
while hq:
time, now = heappop(hq)
for next in road[now]:
dist, rush = road[now][next]
new_time = 0
if rush:
if time <= s:
if time + dist <= s: new_time = dist
else:
new_time = s - time
dist -= new_time
if e - s <= dist * 2:
dist -= (e - s) / 2
new_time += e - s + dist
else:
new_time += dist * 2
elif s < time <= e:
if time + dist * 2 <= e: new_time = dist * 2
else:
new_time = e - time
dist -= new_time / 2
new_time += dist
else:
new_time = dist
else:
new_time = dist
new_time += time
if check[next] > new_time:
heappush(hq,(new_time, next))
check[next] = new_time
result = max(check)
if int(result) == result:
print(int(result))
else:
print(result)
solution()
