https://www.acmicpc.net/problem/31537

| 시간 제한 | 메모리 제한 |
| 1초 | 1024MB |
문제
누구나 그렇듯 동우는 출근하기 싫다. 그래도 출근해야 한다.
동우가 다니는 회사는 신기한 회사이다. 총 N명의 직원이 있는데, 이 중 최대 1명이 출근하지 않아도 업무를 정상적으로 진행할 수 있다. 하지만 1명보다 많이 출근하지 않으면 업무를 정상적으로 진행할 수 없다.
동우는 회사의 업무가 정상적으로 진행되는 것이 신기해 현재 시각으로부터 최근 M시간 동안 N명의 직원 각각이 총 몇 시간씩 출근했는지 살펴보았다.
직원들은 모두 정각에만 출근해 정각에만 퇴근하며, 한 사람이 여러 번 출근 혹은 퇴근할 수 있다. 최근 M시간 동안 업무를 계속 정상적으로 진행할 수 있도록 하는, N명의 직원이 출근한 조합의 경우의 수를 구하시오.
이때, M시간에 대해 매시 30분을 기준으로 출근해 있는 직원들의 목록이 한 번이라도 다른 경우 서로 다른 조합으로 간주한다. 현재는 정각이라 가정한다.
입력
첫 번째 줄에 직원의 수 N과 동우가 살펴본 최근 시간의 길이를 나타내는 정수 M이 공백으로 구분되어 주어진다.
(1 ≤ N, M ≤ 106)
두 번째 줄에 N명의 직원이 최근 M시간 동안 출근한 시간 A1, A2, …, AN이 공백으로 구분되어 주어진다. (0 ≤ Ai ≤ M)
출력
직원이 출근한 조합으로 가능한 경우의 수를 109+7로 나눈 나머지를 출력한다.
단, 109+7은 소수이다.
풀이
1. chatGPT에게 물어보기(잡담)

슬라이딩 윈도우..?
슬라이딩 윈도우 아닌 것 같다니깐
N이 최대 1,000,000인데 지수시간에 비트마스킹 한다고?

슬라이딩 윈도우 아니라니까

chatGPT는 무조건 예스만 말하는 것 같습다.

오... dp? 이 문제의 어려운 버전인 31538번: 출근하기 싫어 2는 dp로 분류되어있긴 합니다.

저는 앳코더에서 chatGPT의 번역 낚시로 여러 번 WA를 받은 경험이 있습니다. 그래서 대 AI시대에 기본적으로 AI를 별로 신뢰하질 않습니다. 솔직히 석사따리에 AI 전문가는 아니지만 강 인공지능도 조만간이라는 힌튼 교수님 말도 별로 믿질 못하겠음... 아마 한국어 모델이 구려서 그렇다고 생각되긴 해요. 근데 이건 좀 너무 심하네.
2. 그냥 직접 생각하기
GPT에게 헬프를 친 이유는 이 문제로 한 이틀 고민하다가 도저히 모르겠어서 물어본 것이었고요. 그럴 수 밖에 없었던 이유가 이 문제 풀이를 아무도 안올렸더라고요. 제4회 고려대 MatKor컵 문제인데 에디토리얼도 없어서 도움 받을 곳이 없었습니다. 근데 그 전에 좀 귀찮아서 생각을 제대로 안해본 것도 있어요. GPT가 이런 똥 프롬프트를 싸버리는 바람에 공책을 펴서 경우의 수를 찬찬히 따져봤습니다.
먼저 전체 출근 가능한 시간대를 하나의 띠로 생각해보겠습니다. 총 M칸의 자리가 나옵니다. 아직까진 아무도 확인하지 않았으니 출근해야 하는 사람이 0명인 상태입니다. 그러니 근무 인원이 부족한 시간대는 없습니다. k명까지 확인했을 때 근무 인원이 k명인 시간대의 수를 p, 근무 인원이 k - 1명인 시간대의 수를 q라고 하겠습니다. M = p + q입니다. 초기 상태는 p = 5, q = 0입니다.
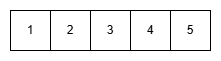
이제 첫 번째 사람의 출근 가능한 시간부터 확인해봅시다. a1시간의 근무가 가능합니다. q의 시간대는 근무 인원이 이미 비어버린 시간이므로 한 명도 더 비어선 안됩니다. a1시간 중 q시간을 먼저 제외시켜줍니다. 그럼 남은 a1-q시간을 p시간에 나눠줄 수 있습니다. 여기서 근무 시간을 배치할 수 있는 방법은 조합으로 구할 수 있습니다. math.comb(p, a1 - q)가 됩니다. 만약 a1이 q보다 작은 경우, 부족한 근무 시간을 채울 수 없게 되고 2명이 근무할 수 없는 시간이 발생해 조건을 만족할 수 없게 됩니다. 곧바로 -1을 출력하고 탐색을 마치도록 합니다.
예제 입력 5에 이걸 적용해보겠습니다.
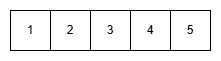
p = 5, q = 0입니다. 먼저 첫 번째 직원은 4시간 근무가 가능합니다. 4 - q의 시간을 p에 분배시켜봅시다. comb(5, 4) = 5입니다. 첫 번째 사람이 근무 시간을 배치하는 방법은 5가지 입니다.

이제 다음 사람은 이 첫 번째 사람의 근무 상태에 따라 배치할 수 있습니다. p = 4, q = 1입니다. 3시간을 배치하기 전, 먼저 이미 비어버린 q시간을 먼저 배치합니다. 이건 q시간을 모두 채워야 하는 1가지만 존재하므로 따로 연산이 필요 없습니다. 이제 배치해야 할 시간은 3 - q = 2시간이 남았고 배치할 시간대는 4시간입니다.
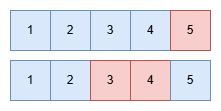
comb(4, 2) = 6입니다. 두 번째 직원은 6가지 방법으로 근무 시간을 배치할 수 있습니다. 이제 5 * 6 = 30가지의 경우가 나왔습니다. p = 3, q = 2입니다. 세 번째 직원은 4시간 근무할 수 있습니다. 먼저 비어버린 q시간을 배치하고 남은 2시간을 3시간에 배치합니다. comb(3, 2) = 3입니다. 5 * 6 * 3 = 60가지의 경우가 나왔습니다.
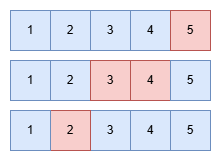
뭐랄까 조합 위에서 다음 조합, 그위에서 또 다음 조합을 돌리는 식이네요.
이제 이걸 코드로 짜보면 파이썬은 시간초과가 뜹니다. 뭔짓을 해도 시간초과입니다. 그 이유는 comb연산이 너무 오래걸리기 때문입니다. 1,000,000까지의 팩토리얼, 나눗셈까지 빠른 시간 내에 해낼 수 있는 방법을 찾아야 합니다. 다행히 문제에서 1e9+7이라는 매우 큰 소수로 결과를 나누도록 하고 있습니다. 모듈로 곱셈 역원을 이용해 조합 연산의 나눗셈을 빠르게 할 수 있습니다.
모듈러 연산의 역원(분수의 모듈러 연산)
1. 모듈러 기본 연산모듈러 연산은 나머지를 구한다. 파이썬에서는 산술 연산자 %와 같다. 10 mod 3 = 10 % 3 = 1. 두 수 a, b에 대해 어떤 수로 모듈러 연산을 했을 때 결과가 같다면 a, b는 모듈러 합동
celbeing.tistory.com
먼저 여러 명의 직원을 탐색하며 팩토리얼 연산을 계속 수행해야 합니다. 어차피 1,000,000이하의 범위에서만 반복적인 곱셈이 이루어질 것이기 때문에 factorial 배열을 만들어 이후에는 연산 없이 팩토리얼 값을 끌어오도록 합시다.
조합 연산은 다음과 같습니다.
comb(n, r) = n! / (r! * (n - r)!)
이 문제에서는 조합 연산 결과를 그대로 사용하는 것이 아니라 mod 1e9+7을 해야 합니다. 이 수는 소수이므로 다음 식을 얻을 수 있습니다. 과정은 길어지니까 그냥 생략할게요. 저는 이론보다 활용이 중요하다고 생각해서...(그냥 귀찮음)
# mod = 1,000,000,007
comb(n, r) % mod = (n! / (r! * (n - r)!)) % mod = (n! * (r! * (n - r)!)mod - 2) % mod
mod - 2승 같은 무시무시한 지수 연산은 빠른 거듭제곱으로 해결해버립시다. 이걸로 팩토리얼의 역원까지 미리 구해놓고 하는 게 시간이 제일 절약되긴 하지만 여기까지만 구현해서 돌려도 pypy3로 통과가 됩니다.
정답 코드
import sys
input = sys.stdin.readline
def solution():
mod = int(1e9 + 7)
factorial = [1] * 1000001
inv_factorial = [1] * 1000001
for i in range(2, 1000001):
factorial[i] = (factorial[i - 1] * i) % mod
def fast_power(n, p):
result = 1
while p:
if p & 1:
result *= n
result %= mod
n **= 2
n %= mod
p >>= 1
return result
def combination(m, p):
result = factorial[m]
k = (factorial[p] * factorial[m - p]) % mod
result *= fast_power(k, mod - 2)
result %= mod
return result
n, m = map(int, input().split())
a = list(map(int, input().split()))
lack = 0
res = 1
for k in a:
if k < lack:
res = 0
break
p = k - lack
res *= combination(m, p)
t = m - p
m -= t
lack += t
res %= mod
print(res)
solution()
https://www.acmicpc.net/problem/31537

| 시간 제한 | 메모리 제한 |
| 1초 | 1024MB |
문제
누구나 그렇듯 동우는 출근하기 싫다. 그래도 출근해야 한다.
동우가 다니는 회사는 신기한 회사이다. 총 N명의 직원이 있는데, 이 중 최대 1명이 출근하지 않아도 업무를 정상적으로 진행할 수 있다. 하지만 1명보다 많이 출근하지 않으면 업무를 정상적으로 진행할 수 없다.
동우는 회사의 업무가 정상적으로 진행되는 것이 신기해 현재 시각으로부터 최근 M시간 동안 N명의 직원 각각이 총 몇 시간씩 출근했는지 살펴보았다.
직원들은 모두 정각에만 출근해 정각에만 퇴근하며, 한 사람이 여러 번 출근 혹은 퇴근할 수 있다. 최근 M시간 동안 업무를 계속 정상적으로 진행할 수 있도록 하는, N명의 직원이 출근한 조합의 경우의 수를 구하시오.
이때, M시간에 대해 매시 30분을 기준으로 출근해 있는 직원들의 목록이 한 번이라도 다른 경우 서로 다른 조합으로 간주한다. 현재는 정각이라 가정한다.
입력
첫 번째 줄에 직원의 수 N과 동우가 살펴본 최근 시간의 길이를 나타내는 정수 M이 공백으로 구분되어 주어진다.
(1 ≤ N, M ≤ 106)
두 번째 줄에 N명의 직원이 최근 M시간 동안 출근한 시간 A1, A2, …, AN이 공백으로 구분되어 주어진다. (0 ≤ Ai ≤ M)
출력
직원이 출근한 조합으로 가능한 경우의 수를 109+7로 나눈 나머지를 출력한다.
단, 109+7은 소수이다.
풀이
1. chatGPT에게 물어보기(잡담)

슬라이딩 윈도우..?

슬라이딩 윈도우 아닌 것 같다니깐

N이 최대 1,000,000인데 지수시간에 비트마스킹 한다고?

슬라이딩 윈도우 아니라니까

chatGPT는 무조건 예스만 말하는 것 같습다.

오... dp? 이 문제의 어려운 버전인 31538번: 출근하기 싫어 2는 dp로 분류되어있긴 합니다.

저는 앳코더에서 chatGPT의 번역 낚시로 여러 번 WA를 받은 경험이 있습니다. 그래서 대 AI시대에 기본적으로 AI를 별로 신뢰하질 않습니다. 솔직히 석사따리에 AI 전문가는 아니지만 강 인공지능도 조만간이라는 힌튼 교수님 말도 별로 믿질 못하겠음... 아마 한국어 모델이 구려서 그렇다고 생각되긴 해요. 근데 이건 좀 너무 심하네.
2. 그냥 직접 생각하기
GPT에게 헬프를 친 이유는 이 문제로 한 이틀 고민하다가 도저히 모르겠어서 물어본 것이었고요. 그럴 수 밖에 없었던 이유가 이 문제 풀이를 아무도 안올렸더라고요. 제4회 고려대 MatKor컵 문제인데 에디토리얼도 없어서 도움 받을 곳이 없었습니다. 근데 그 전에 좀 귀찮아서 생각을 제대로 안해본 것도 있어요. GPT가 이런 똥 프롬프트를 싸버리는 바람에 공책을 펴서 경우의 수를 찬찬히 따져봤습니다.
먼저 전체 출근 가능한 시간대를 하나의 띠로 생각해보겠습니다. 총 M칸의 자리가 나옵니다. 아직까진 아무도 확인하지 않았으니 출근해야 하는 사람이 0명인 상태입니다. 그러니 근무 인원이 부족한 시간대는 없습니다. k명까지 확인했을 때 근무 인원이 k명인 시간대의 수를 p, 근무 인원이 k - 1명인 시간대의 수를 q라고 하겠습니다. M = p + q입니다. 초기 상태는 p = 5, q = 0입니다.

이제 첫 번째 사람의 출근 가능한 시간부터 확인해봅시다. a1시간의 근무가 가능합니다. q의 시간대는 근무 인원이 이미 비어버린 시간이므로 한 명도 더 비어선 안됩니다. a1시간 중 q시간을 먼저 제외시켜줍니다. 그럼 남은 a1-q시간을 p시간에 나눠줄 수 있습니다. 여기서 근무 시간을 배치할 수 있는 방법은 조합으로 구할 수 있습니다. math.comb(p, a1 - q)가 됩니다. 만약 a1이 q보다 작은 경우, 부족한 근무 시간을 채울 수 없게 되고 2명이 근무할 수 없는 시간이 발생해 조건을 만족할 수 없게 됩니다. 곧바로 -1을 출력하고 탐색을 마치도록 합니다.
예제 입력 5에 이걸 적용해보겠습니다.

p = 5, q = 0입니다. 먼저 첫 번째 직원은 4시간 근무가 가능합니다. 4 - q의 시간을 p에 분배시켜봅시다. comb(5, 4) = 5입니다. 첫 번째 사람이 근무 시간을 배치하는 방법은 5가지 입니다.

이제 다음 사람은 이 첫 번째 사람의 근무 상태에 따라 배치할 수 있습니다. p = 4, q = 1입니다. 3시간을 배치하기 전, 먼저 이미 비어버린 q시간을 먼저 배치합니다. 이건 q시간을 모두 채워야 하는 1가지만 존재하므로 따로 연산이 필요 없습니다. 이제 배치해야 할 시간은 3 - q = 2시간이 남았고 배치할 시간대는 4시간입니다.

comb(4, 2) = 6입니다. 두 번째 직원은 6가지 방법으로 근무 시간을 배치할 수 있습니다. 이제 5 * 6 = 30가지의 경우가 나왔습니다. p = 3, q = 2입니다. 세 번째 직원은 4시간 근무할 수 있습니다. 먼저 비어버린 q시간을 배치하고 남은 2시간을 3시간에 배치합니다. comb(3, 2) = 3입니다. 5 * 6 * 3 = 60가지의 경우가 나왔습니다.

뭐랄까 조합 위에서 다음 조합, 그위에서 또 다음 조합을 돌리는 식이네요.
이제 이걸 코드로 짜보면 파이썬은 시간초과가 뜹니다. 뭔짓을 해도 시간초과입니다. 그 이유는 comb연산이 너무 오래걸리기 때문입니다. 1,000,000까지의 팩토리얼, 나눗셈까지 빠른 시간 내에 해낼 수 있는 방법을 찾아야 합니다. 다행히 문제에서 1e9+7이라는 매우 큰 소수로 결과를 나누도록 하고 있습니다. 모듈로 곱셈 역원을 이용해 조합 연산의 나눗셈을 빠르게 할 수 있습니다.
모듈러 연산의 역원(분수의 모듈러 연산)
1. 모듈러 기본 연산모듈러 연산은 나머지를 구한다. 파이썬에서는 산술 연산자 %와 같다. 10 mod 3 = 10 % 3 = 1. 두 수 a, b에 대해 어떤 수로 모듈러 연산을 했을 때 결과가 같다면 a, b는 모듈러 합동
celbeing.tistory.com
먼저 여러 명의 직원을 탐색하며 팩토리얼 연산을 계속 수행해야 합니다. 어차피 1,000,000이하의 범위에서만 반복적인 곱셈이 이루어질 것이기 때문에 factorial 배열을 만들어 이후에는 연산 없이 팩토리얼 값을 끌어오도록 합시다.
조합 연산은 다음과 같습니다.
comb(n, r) = n! / (r! * (n - r)!)
이 문제에서는 조합 연산 결과를 그대로 사용하는 것이 아니라 mod 1e9+7을 해야 합니다. 이 수는 소수이므로 다음 식을 얻을 수 있습니다. 과정은 길어지니까 그냥 생략할게요. 저는 이론보다 활용이 중요하다고 생각해서...(그냥 귀찮음)
# mod = 1,000,000,007
comb(n, r) % mod = (n! / (r! * (n - r)!)) % mod = (n! * (r! * (n - r)!)mod - 2) % mod
mod - 2승 같은 무시무시한 지수 연산은 빠른 거듭제곱으로 해결해버립시다. 이걸로 팩토리얼의 역원까지 미리 구해놓고 하는 게 시간이 제일 절약되긴 하지만 여기까지만 구현해서 돌려도 pypy3로 통과가 됩니다.
정답 코드
import sys
input = sys.stdin.readline
def solution():
mod = int(1e9 + 7)
factorial = [1] * 1000001
inv_factorial = [1] * 1000001
for i in range(2, 1000001):
factorial[i] = (factorial[i - 1] * i) % mod
def fast_power(n, p):
result = 1
while p:
if p & 1:
result *= n
result %= mod
n **= 2
n %= mod
p >>= 1
return result
def combination(m, p):
result = factorial[m]
k = (factorial[p] * factorial[m - p]) % mod
result *= fast_power(k, mod - 2)
result %= mod
return result
n, m = map(int, input().split())
a = list(map(int, input().split()))
lack = 0
res = 1
for k in a:
if k < lack:
res = 0
break
p = k - lack
res *= combination(m, p)
t = m - p
m -= t
lack += t
res %= mod
print(res)
solution()
