https://www.acmicpc.net/problem/18858

| 시간 제한 | 메모리 제한 |
| 1초 | 1024MB |
문제
훈련소로 가는 날 욱제는 문득 떠올렸다. 훈련소가 논산에 있는 이유는 무엇일까? 왜 why?
그것은 바로…
논산(non-산)은 산이 아니기 때문이다. 길이가 3인 수열 a1, a2, a3가 산임은 a1 < a2 > a3임을 의미한다. 어떤 수열이 논산임은 수열의 인접한 세 항이 산인 경우가 없음을 의미한다. 다시 말해, 길이 N의 수열 a에 대해 2 ≤ i < N 이고 ai-1 < ai > ai+1인 경우가 없다.
논산인 수열이 몇 개가 있는지 알아보자.
입력
첫째 줄에 N과 M이 주어진다.
- 1 ≤ N ≤ 1,000
- 1 ≤ M ≤ 100
출력
1 이상 M 이하의 정수로 이루어진 길이 N의 수열 중 논산인 것의 개수를 998,244,353으로 나눈 나머지를 출력한다.
풀이
길이가 3인 수열이 산이라 함은 가운데 값이 크니까 증가 이후에 감소가 따라오는 것으로 생각해서 접근했습니다. 그래서 시작부터 끝까지 증가하지 않는 수열, 감소하지 않는 수열의 수를 구하면 되겠구나! 근데 아니었구요.
이런 예외가 있습니다. 길이 3인 산인 수열의 정의는 가운데 값이 양 끝값보다 크기만 하면 됩니다. 만약 길이가 4인 수열이 [3, 5, 5, 4] 와 같은 형태로 있다면, 값 자체로는 산처럼 보이지만 길이가 3인 어느 구간([3, 5, 5], [5, 5, 4])에도 산인 구간은 없게 됩니다. 따라서 단순히 증가하지 않는 수열, 감소하지 않는 수열만 구하면 문제에서 요구하는 값보다 적은 값이 나오게 됩니다.
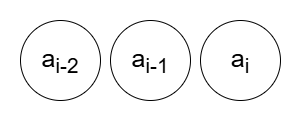
새로 추가할 i번째 값을 놓고 생각해봅시다. 바로 앞에 놓인 두 값이 어떤 관계이냐에 따라 i번째 값에 어떤 수 k가 올 수 있는지 없는지가 결정됩니다.
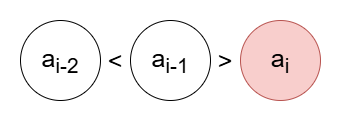
이렇게 i-2번째 값보다 i-1번째 값이 크다면 i번째 값은 i-1번째 값보다 작아서는 안됩니다.
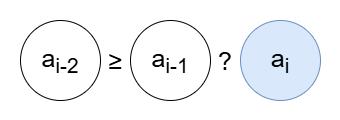
하지만 i-2번째 값이 i-1번째 값보다 크거나 같기만 하다면 i번째 값은 어떤 값이 와도 상관이 없습니다. 이제 수열의 상태를 둘로 나누어 보겠습니다.
- 직전 2개의 값이 증가 관계인 수열 inc
- 직전 2개의 값이 증가 관계가 아닌 수열 non_inc
각 수열은 2차원 배열로, 두 가지 값을 인덱스로 관리되어야 합니다. 첫째는 수열의 길이 i입니다. 둘째는 마지막에 쓰인 값 j입니다. 그럼 점화식을 이렇게 써볼 수 있습니다.
$inc[i][j]\;=\;\sum_{k=1}^{j-1}inc[i-1][k]$
$non\_inc[i][j]\;=\;\sum_{k=1}^{m}non\_inc[i-1][k]$
길이 1부터 순차적으로 구성해나가면서 마지막에 inc[n] 전체와 non_inc[n] 전체의 합을 출력하면됩니다.
아 물론 모든 처리과정에 998,244,353로 나눈 나머지를 저장합니다.
정답 코드
code
