
1. 충족가능성 문제(Boolean satisfiability problem, SAT)
여러 변수로 논리 값들이 주어졌을 때, 그 논리 값들로 이루어진 식이 참이 되는 논리 값의 상태가 존재하는가에 대한 문제입니다. 이거 약간 뭐랑 비슷하냐면 대학교 시간표 짜는 거랑 비슷합니다. 작년 연구부장 역임했던 바로 생각해보면 전담 시간표 짜는게 딱 이 SAT 문제 입니다. 제가 일반 종합대학을 다녀본 경험이 없으니 그냥 교육대학교에서 만났던 과목으로 생각해봅시다. (제가 다녔던 대학교는 사실 수강신청이랄 것도 없긴 했습니다. 그냥 예시 만들기 어려우니까 그런갑다 해봅시다.)
개설되는 다음 4개의 과목을 조건에 맞게 수강할 수 있는 방법이 있을까요?
- 교육심리(A)와 교육철학(B) 중 한 과목은 반드시 수강해야 한다.
- 교육심리(A)를 수강하면 교육행정(C)을 반드시 수강해야 한다.
- 교육철학(B)과 교육행정(C)은 동시에 수강할 수 없다.
- 교육철학(B)를 수강하면 교육사회학(D)을 반드시 수강해야 한다.
- 교육사회학(D)을 수강하면 교육심리(A)를 반드시 수강해야 한다.
각 조건을 논리식으로 표현해보면 이렇습니다.
- A와 B 둘 중 하나는 반드시 수강해야 한다. → A∨B
- A를 수강하면 C를 반드시 수강해야 한다. = A가 선택되지 않은게 아니라면 C가 반드시 선택되어야 한다. → ¬A∨C
- B와 C는 동시에 수강할 수 없다. = B가 선택되지 않거나 C가 선택되지 않아야 한다. → ¬B∨¬C
- B와 D 둘 중 하나는 반드시 수강해야 한다. → B∨D
- D를 수강하면 A를 반드시 수강해야 한다. = D가 선택되지 않은게 아니라면 A가 반드시 선택되어야 한다. → ¬D∨A
5가지 조건은 모두 True여야 합니다. 그럼 수강 가능성 X는 이런 논리식으로 정리할 수 있습니다.
X = (¬A∨C)∧(¬B∨¬C)∧(B∨D)∧(¬D∨A)
몇 번의 시도를 해본다면 X가 True가 될 가능성이 있는지 확인해볼 수 있습니다. 첫 번째 절에 의해 A = True라면 C = True여야 합니다. 두 번째 절에 의해 C = True라면 B = False여야 합니다. 세 번째 절에 의해 B = False라면 D = True여야 합니다. 네 번째 절은 D = True, A = True로 True입니다. 그러면 모든 절이 True로 만들어지며 X = True인 상태가 존재합니다.
2. 2-SAT와 SCC
SAT는 각 절마다 논리 값을 몇 개로 제한하느냐에 따라 k-SAT로 불립니다. k = 1은 여기서 의미가 없고, k > 2인 모든 SAT는 다항시간 내에 3-SAT로 환산이 가능하다고 합니다. 원리는 모르지만 일단 그렇답니다. 3-SAT는 아직 효율적인 풀이 알고리즘이 없지만 앞서 예시로 들었던 논리식 형태로 표현되는 2-SAT는 있습니다. 지난 번에 정리한 강한연결요소(SCC)를 통해 2-SAT를 풀 수 있습니다.
첫 번째 절을 보면 ¬A∨C = True여야 합니다. 그렇다면 A = True일 때 C가 반드시 True여야 하고(A→C), C = False일 때, A가 반드시 False여야 합니다.(¬C→¬A) (반대는 성립하지 않는 경우가 있습니다.) 각 논리 상태를 정점으로 두고 연결하면 다음과 같이 표현할 수 있습니다.
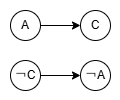
모든 절에서 이렇게 두 가지 간선이 나옵니다. 이제 A~D의 모든 논리 상태를 논리식에 따라 표현해보겠습니다.

복잡하니까 정점 위치를 좀 깔끔하게 바꾸겠습니다.
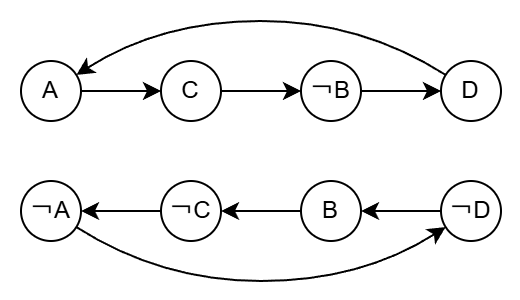
유향 그래프가 하나 만들어졌습니다. 그래프를 들여다보면 SCC가 있음을 알 수 있습니다. SCC를 구성해 표시해보겠습니다.
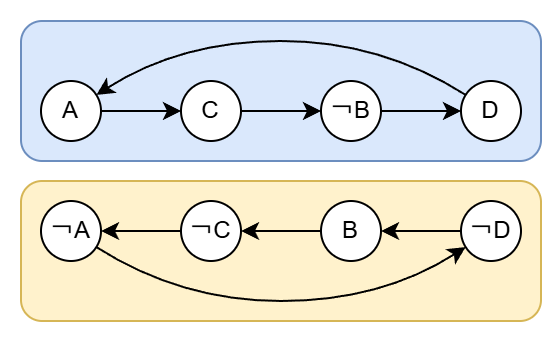
각각의 SCC가 포함하고 있는 컴포넌트를 살펴보았을 때 어떤 명제 x와 그 역인 ¬x가 동시에 들어있다면 그 SCC는 선택될 수 없습니다. 즉 충족 가능성이 없게 됩니다. 이렇게 주어진 조건에 따라 명제로 그래프를 구성하여 SCC를 추출하는 것으로 2-SAT 문제의 충족여부를 확인해볼 수 있습니다.
